Abstract: 本文以线性变换的角度重新理解矩阵变换的原理,以对角化和SVD作为主要的案例
Keywords: Diagonalization,Pseudoinverse
对角化和伪逆
傻子不是生出来的,是教出来的,如果一个人从小没人教他如何看问题如何思考,或者他自己也不愿意去思考,别人说什么他都相信,那么这个人将会变成一个温和的劳动者,这个道理我们老一辈革命家们都明白,枪杆子笔杆子就可万世而为君,看个头条都能热血沸腾的人统治成本极低。
对角化和伪逆(Diagonalization and the Pseudoinverse)
首先我们要回顾下,并且强调下昨天讲的内容,就是线性变换对应的矩阵,对于不同空间相互变换,知道空间是不能确定矩阵的,还要确定基和相互关系,光知道基也没用,比如求导和求积分的例子告诉我们,必须要知道他们之间的计算关系,或者叫做原始空的基向量线性变换到目标空间后的向量是啥才能确定矩阵A(上一篇的🌰 1)。
接下来的换基运算是在同一个空间下进行的,也就是线性变换后空间不变,空间不变以为这矩阵的Rank不发生变化,想要进行换基操作就要知道新的基和原来的基都分别是什么,然后就能确定出矩阵了。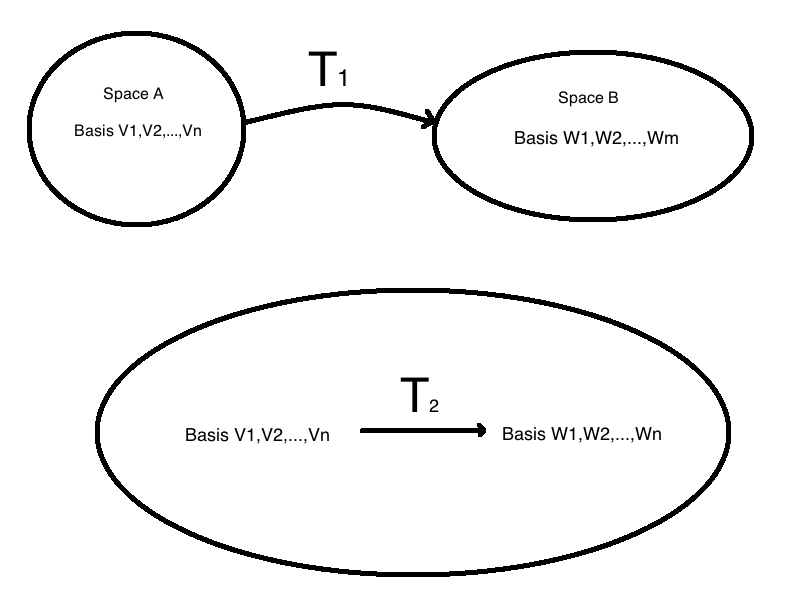
手工图片,简约而不简单,哈哈,$T_1$就是个典型的夸空间的变换,已知两组基 $\vec{v_n}$ 和 $\vec{w_m}$ 并且要明确的知道 $T(\vec{v_n})$ 是啥,这样才能确定$T_1$ 对应的变换矩阵A是啥。
但是对于$T_2$ 就没有后面的要求了,只要知道两组基 $\vec{v_n}$ 和 $\vec{w_n}$ 就可以确定出$T_2$ 对应的变换矩阵A了;
上面是一个简单的回顾,也是上一篇的高度概括,主要在求变换矩阵上,每个矩阵都对应一个变换,如果已知输入空间,那么根据这个矩阵可以得到一个线性变换的输出空间,我们所有使用到矩阵乘法的地方都可以看成线性变换的过程,当然其中一部分也可以当做换基操作,我们下面的主要研究集中在换基上,也就是同一个空间下的形式转换。
本课程最前面有一句话,就是我们天天变成三角矩阵也好对角矩阵也好,就是为了让矩阵形式变得简单同时,暴露出矩阵的性质(类似于大数据挖掘),而这些所有对角化,消元操作对应的都是矩阵乘法,也即是说,我们可以通过换基来使矩阵变得漂亮(上一篇说过),我们今天就看看怎么通过换基让矩阵变得简洁漂亮。
因为变换太多了,我们找两个厉害的,对角化和SVD来讲解
在讲解之前我们有必要对矩阵和向量相乘进行下分析,下面假设A可逆:
$$
w=A\vec{v}
$$
这里面我们规定 $\vec{v}$ 的基是标准基,就是$I$ ,那么 $w$ 的基就是 $A^{-1}$ ,为什么,下面我们开动想象,我们说向量有大小有方向,所以我们用一个有序的数字串来表示一个向量,但是这里隐含的是在坐标系是标准坐标系的情况下,那么我们一旦更换坐标系,变换的是这串数字,向量本身的方向大小不变,也就是说指向南方的长度为1的向量,可以有不同的无数组有序数字串表示,也就是基于不同的基。
所以上面的v到w的线性变换就是换基,根据我们前面的例子,可以得知这矩阵A线性变换后的基是$A^{-1}$ 的列向量,如果我们继续我们的变换也就是
$$
w’=Bw=BA\vec{v}
$$
这个连续的线性变换的过程是$\vec{v}$作为输入先通过A到输出中,也就是w,然后以这个输出作为输入,经过B得到B的输出空间。注意先A后B,在乘法中表现为 $BA$ 。
注意上面我们并没有左边的矩阵,也就是没有等效矩阵,接下来我们引入C,$C=BA$ 那么我们就有:
$$
w’=Bw=BA\vec{v}=C\vec{v}\\
C\vec{v}=BA\vec{v}
$$
如果我们更严谨一些把省略掉的标准基补充进来的话 $\vec{v}=I\dot{v}$ 是最正确的写法,我们这里不需要默认 $\dot{v}$ 的基是什么,他现在就是一个没有基的数组了(也不是向量),但是单独说v没有意义,必须$Iv$ 才有意义,那么上面的式子将变成:
$$
CI\dot{v}=BAI\dot{v}\\
CI=BAI
$$
我们这里研究一下$BAI$,我们首先得到的是标准基的输出(通过与$I$相乘),然后我们得到A的输出(通过与 $A$ 相乘),最后我们得到B的输出(通过与 $B$ 相乘),上述所有的输入都是上一步的输出。
所以上面的整个过程可以分解成下面这幅图: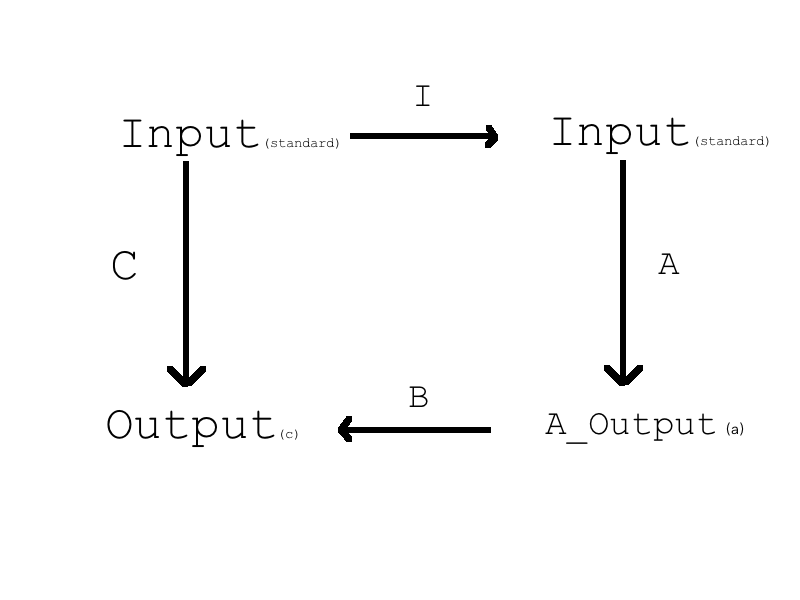
整个换基过程就是这样被拆解的,但是面对不同的拆解方式,我们可能得到非常标量的A,这个是我们想要的,也就是C被分解了,分解出了漂亮的A,我们对矩阵的所有操作基本都是在干这个事,所以这些事都算换基操作,整个过程就是当标准基输入到C中我们可以得到输出,这个过程的等效过程是先输入漂亮的A然后得到的输出再输入到B最后得到的输出和C的输出一致。
要说明的是上面的箭头方向对应一个矩阵,如果这个矩阵可逆那么这个箭头就可以反过来对应的矩阵也就变成了原矩阵的逆。
相似矩阵 :$A$ and $S^{-1}AS$ and $W^{-1}AW$
还是我们上面$C=BA$ 的分解过程,那么把它变形到其他矩阵分解形式,对角化或者相似矩阵和上面的比较相似,举个🌰
$$
B=M^{-1}AM\\
$$
如果我们已知B,那么如果A很漂亮,这个换基过程就很值得了
首先从标准基换到 $M^{-1}$ 为基的空间(首先要从又开始上面说为啥了,为啥是$M^{-1}$ 前面有说过,$M^{-1}$ 的每一列都是基,因为M可逆所以必然线性无关)得到的输出作为输入,输入到漂亮A,然后的输出是漂亮A所对应的基,然后再通过$M^{-1}$ 回到以M的每列为基的形式,这个过程出来的矩阵被定义为相似的,当M对应的是特征向量,那么漂亮A改名 $\Lambda$ 这个矩阵足够漂亮到所有人都喜欢他.
不同的M可以得到不同的漂亮A,下面我们看看🌰
eg. Project onto the line $y=-x$ that goes from northwest to southeast. The vector $(1,0)$ projects to $(.5,.5)$ ,the projection of $(0,1)$ is $(-.5,.5)$
- 按照标准做法,选取标准基,我们可以得到线性变换矩阵 $A=\begin{bmatrix}.5&-.5\newline -.5&.5\end{bmatrix}$ 。
- 如果我们想要对角矩阵,需要先求出特征向量矩阵 $S=\begin{bmatrix}1&1\newline-1&1\end{bmatrix}$ 对应的求出在 $S^{-1}$ 基下的线性变换矩阵 $\Lambda=\begin{bmatrix}1&0\\0&0\end{bmatrix}$ 果然很漂亮然后把输出再变换到$S$ 为基的形式就回到了上面的A
- 求相似和2类似这里不再赘述
上面的过程对于线性变换$T$ 对应矩阵A,我们可以通过一系列的换基操作在其他基下找到等效的但是比A漂亮的矩阵,再通过换基操作还原到A基形式下,这个过程就是$IAI=W^{-1}XW$ 的各种特例。
奇异值分解(SVD)
与上面的最大不同,SVD输入输出来自两个空间,我们上面说在同一空间下的线性变换都是换基操作,这里展示不同空间的换基操作,神奇的SVD,对于不同空间的线性变换矩阵,一般为长方形的(参考求导和微分的例子,在上一篇),假设矩阵A可以完成一个跨空间的线性变换,那么当我们改变两个空间的基的时候,这个时候,奇迹就发生了,当我们把原始空间X(dim=n)的基从标准基变成$AA^T$特征向量,得到一个换基后的输入,然后我们再把原始出Y(dim=m)换基到成$A^TA$特征向量,作为目标矩阵的输入和输出,那么我们会得到一个漂亮的对角矩阵(对角元素可能是0)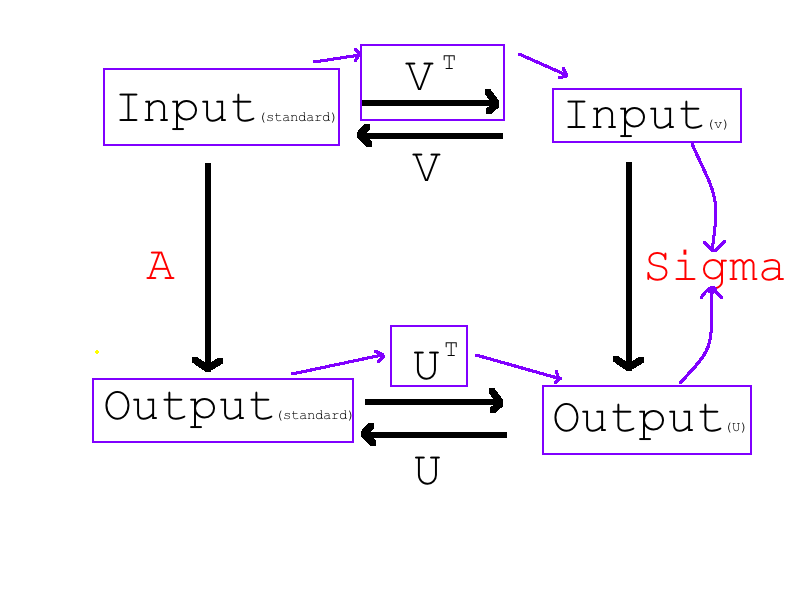
上面这个求解 $\Sigma$ 的过程并不是一根筋,而是两头堵,根据紫色线的方向求解的,因为U和V都是正交矩阵,所以其逆和转置一样。
伪逆(The Pseudoinverse)
伪逆就是不是真的逆,并不是所有矩阵都有逆,但是所有矩阵都有伪逆,当矩阵是可逆矩阵的时候,伪逆和逆相等,我们前面学四个子空间的时候学过一幅图:
这幅图我们当时有详细讲解,假设矩阵是 $m\times n$ 的那么他的行空间和Nullspace加起来肯定是$\Re^n$ ,文中已证明,这个也是线性代数的基本定理,那么 $\Re^n$ 中的任何向量都能被分解成rowspace和nullspace中基的线性组合,所以线性映射后得到将是列空间中的一个向量加上0,所以当nullspace不止零向量的时候不可逆,因为nullspace不能被反射,但是这里有个有趣的就是$Ax_r=b$ 可以被反射得到输入向量的rowspace的分量$x_r$,这个反射矩阵就是Pseudoinverse。
从换基的角度,继续SVD,我们看到上图我们走的紫色路线,那么我们如果想反着走: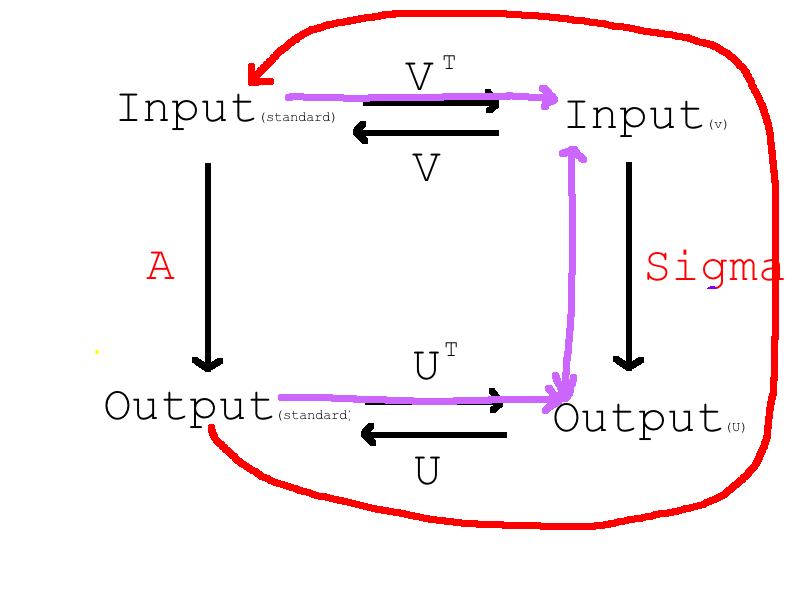
红线对应的就是A的伪逆(如果A是可逆的也可能是逆),我们采取和求$Sigma$ 同样的两头堵占略,根据紫色的大粗箭头的方向进行换基,能够求到 $\Sigma_r^{-1}$ (只有r个有效成分),然后我们跟着红色箭头的方向就能得到A的伪逆了$A^{+}$ :
$$
\Sigma_r^{-1}=
\begin{bmatrix}
\sigma_1^{-1}&&\\
&\ddots&\\
&&\sigma_r^{-1}
\end{bmatrix}\\
\Sigma^{+}=
\begin{bmatrix}
\sigma_1^{-1}&&&&&\\
&\ddots&&&&\\
&&\sigma_r^{-1}&&&\\
&&&0&&\\
&&&&\ddots&\\
&&&&&0
\end{bmatrix}
$$
然后
$$
\Sigma^{+}\Sigma =
\begin{bmatrix}
1&&&&&\\
&\ddots&&&&\\
&&1&&&\\
&&&0&&\\
&&&&\ddots&\\
&&&&&0
\end{bmatrix}
$$
然后顺势就能求出$A^{+}$ 了整个过程如此,不在计算验证。把书上反射的图也贴上,大家对比来看:
然后总结下我们学过的所有的变换的换基角度:
Conclusion
至此,线性代数的基础理论部分算是完结了,我们接下来可能介绍线性代数的一些相关应用,也有可能增加复数矩阵部分,但是不作为这个系列的内容了,所以我们线性代数今天正式毕业!撒花,啦啦啦,但是后面还有更精彩的系列,敬请关注!
