Abstract: 本篇介绍线性代数的另一个角度,就是线性变换思想
Keywords: Linear Transformation,Linear Combination,Kernel,Range
线性变换思想
线性代数到上一篇可以说已经成体系了,不能说自己精通,起码了解了大概的讨论,接下来这三篇第7章的博客是从另一个角度入门线性代数,所以从现在开始,你可以忘记前面学的所有的切入方法,也就是线性代数提出的方法,我们之前的完整套路依靠的是对线性方程组求解的过程引出后面一系列的操作,但是,线性代数为什么叫线性代数,而不叫线性方程组呢?那么本章就是解释,我觉得这个角度切入提出完整的理论更通顺,但是问题就是这么切入没有通过方程组来的那么简单,所以这个角度适合下一步提高,线性方程组适合入门,但是殊途同归,最后都能得到完整的线性代数知识框架。
线性变换思想(The Idea of a Linear Transformation)
我们第一章应该反复强调线性组合,就是一个乘加计算满足线性,当时一直很困惑为啥叫线性组合,并且当时的博客一直强调线性组合是线性代数的重要理论基础,有了线性组合才有了后面的所有。但是线性组合和线性变换有所区别:线性组合是线性变换的一种,但是线性变换并不一定就是乘加计算(线性组合)。从Caculus的角度来看,如果把某个线性组合看成一个函数,那么这个函数 $T$ 满足 :
$$
T(x+y)=T(x)+T(y)\\
T(\alpha x)=\alpha T(x)
$$
或者
$$
T(\alpha x + \beta y)=\alpha T(x) + \beta T(y)
$$
这两种表达方式都是在Caculus中对函数线性的表达,如果对于线性代数,我们应该把输入输出转换到对应的向量空间,$T$ 不在表示一个number to number的映射,而是一个vector to vector的映射:
A Transformation T assigns an output $T(v)$ to each input vector $v$ in $V$. The transformation is linear if it meets these requirement for all $\vec{v}$ and $\vec{w}$:
$$
T(v+w)=T(v)+T(w)\\
T(cv)=cT(v)
$$
or take the two equation into one:
$$
T(cv+dw)=cT(v)+dT(w)
$$
接下来正经的做法是举例子,但是我想让大家都冷静冷静,当年张三丰教张无忌太极剑法的时候,就问张无忌忘了多少了?张教主说忘了一半了,又过了一会儿,张教主说全忘了,于是张真人说甚好,去揍他吧。哈哈,这段话说的基本上就是一个知识理解的必要过程,如果这段知识,你的师父或者教材让你很流畅的读下来,你肯定啥都记不住,因为一切太通常,你回觉得一切都那么理所当然,而蹩脚的老师讲的课会让你听了之后印象深刻,因为每个地方都有不懂的,你就会思考所以印象深刻,这种印象深刻的最直接后果就是等你忘了以后就真的忘了,而大师讲的课,你可能忘得更快,但是当你再看第二遍的时候整个知识树瞬间全部连接起来,融汇贯通,印象最深刻的一个坑爹老师是高中的一个生物老师,说实话,不客气的说那个老师真的是高中遇到最垃圾的老师,当时高中我还是个积极上进的好学生,每天还在思考上清华还是上北大呢,结果这个老师让我第一次知道什么是垃圾的老师,上课念课本不说,完全没有自己的体系,然后每天的方式就是提问不会的要被罚写(每个概念20遍,然后我用五只笔捆绑在一起,然后瞬间完成),卧槽,我当时都震惊了,还有这种教课方式,好在后来可爱的海燕老师来了,这个货就滚蛋了,不然我估计我连西电都考不上。
怎么样,现在还能想起来矩阵怎么来的么?如果还能想起来上面那么一大段废话就白说了,赶紧忘了矩阵,我们现在没有矩阵,只有线性变换。
举个🌰 :
如果$T(v)=v$ 那么,我们就有了一个极为特殊的例子,也就是说输入空间的向量和输出向量一致,那么输入空间V和输出空间W也就是一致的,这里引出了输入输出空间。
举另外一个🌰 :
$$
T(v)=Av+u_0
$$
我们先忽略那个A,告诉自己这不是矩阵不是矩阵不是矩阵,这就是个参数,大写的参数,。
那么
$$
T(v+w)=Av+Aw+u_0 \neq Av+u_0+Aw+u_0=T(v)+T(w)
$$
很明显这不是一个线性变换,这是一个线性变换$Av$ 然后sift了一下(linear-plus-shift),我们管这个叫做放射变换(Affine)在图像处理里面经常用到。
线到线,三角到三角(Lines to Lines,Triangles to Triangles)
尘归尘土归土,经过线性变换,直线依旧是直线,这就是这个section要说的,也就是一个例子,然后这个例子表明为啥叫做线性变换,直线经过变换依旧是直线。
如何证明直线经过线性变换还是直线呢,我们知道两个点可以确定一个直线,那么我们假设点$a(x_1,y_1)$ 在直线上, 点$b(x_2,y_2)$ 在直线上,那么直线上的中点,可以表示为$c(\frac{1}{2}x_1+ \frac{1}{2}x_2,\frac{1}{2}y_1+ \frac{1}{2}y_2)$ 也就是说对于两个点确定的直线上的中点经过线性变换,如果依然是这两个点的中点,那么直线经过线性变换还是直线:
$$
c’=\frac{1}{2}T(a)+\frac{1}{2}T(b)=T(\frac{1}{2}a+\frac{1}{2}b)=T(c)
$$
这就证明了直线上两个给定点的中间点经过线性变换还是变换后的直线的中间点,也就是说$c$经过变换后还是$a,b$ 的中点,迭代下去可以证明$a,c$的中间点$c’$, $a,c’$ 的中间点$c’’$ 以此迭代下去最终得到极限情况下,直线经过线性变换后依旧是直线。
整理下上面的凌乱的过程,我们为了证明直线经过线性变换后还是直线,那么就证明直线上两点之间的点,经过线性变换后还是这两个点(变换后的)的中点,那么递归的证明下去,整个直线依旧是直线,就这样了。
不太懂的看看图吧: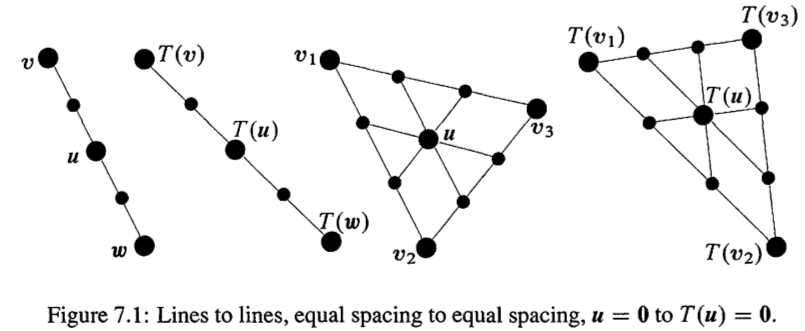
图上把三角形也画出来了,道理跟上面直线的一样,线性变换后点到对应的点上去,直线还是直线,所以三角形也能保持还是三角形。只是形状和方向发生了变化。
线性变换的扩展,对于多个向量:
$$
u=c_1v_1+c_2v_2+\dots + c_nv_n\\
T(u)=c_1T(v_1)+c_2T(v_2)+ \dots + c_nT(v_n)
$$
对于线性变换,也有一套独立的术语,比如对于一个线性变换 $T(v)=Av$ (A不是矩阵,不是矩阵不是矩阵),那么$T(v)=0$ 成立的 $v$ 叫做”Kernel” ;所有的输出$T(v)$ 被称作”range”
。对应的就是nullspace和columnspace不过我们只叫他们kernel或者range,因为我们还没给出矩阵的定义,下篇才会给出。
平面线性变换(Linear Transformation of the Plane)
这里还是一个大🌰 ;但是看起来比较可爱,证明过程上面证明直线的时候已经证明了,但是这里有个小问题,就是他又用矩阵了,我这篇中极力的避免矩阵,因为我们还没证明线性变换跟矩阵什么关系,但是我们不妨假设矩阵 $A$ 对向量空间 $V$ 的变换是线性的,所以我们的小房子就要变形了: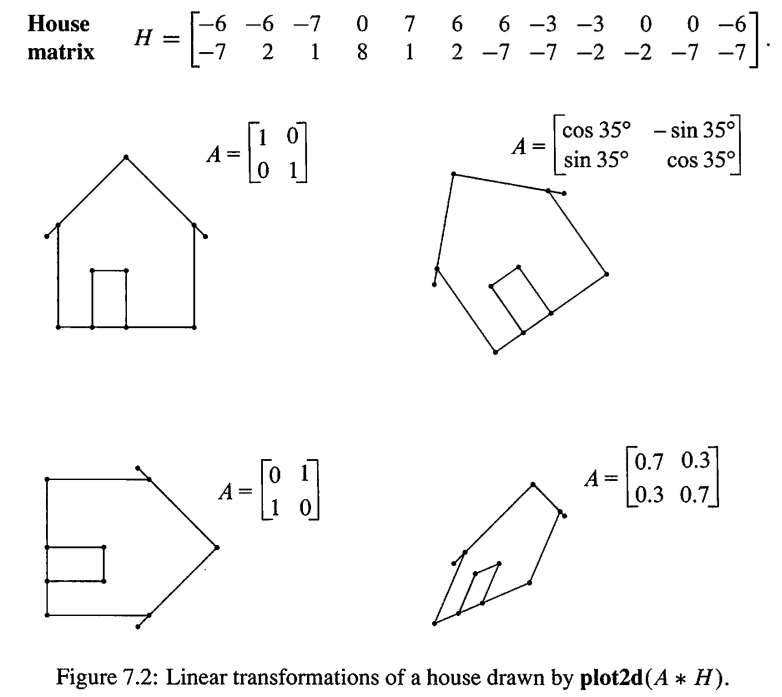
Conclusion
总结就是今天要把线性变换和后面矩阵引出的部分写完,然后我就可以高高兴兴的搞概率论了,线性代数的基础部分也就算是毕业了,待续。。
