Abstract: 本篇介绍正交性,向量正交,矩阵正交,子空间正交
Keywords: Orthogonality,Four Subspace,Orthogonal Complements,Fundamental Theorem of Linear Algebra ,Combining Bases from Subspaces,Split
四个正交子空间
正交
这个地方大师Gilbert写了关于$Ax$的三个境界:
- This is only a number
- It is combination of column vectors
- It shows Subspaces
这个跟王国维的人生三大境界有的一拼,这里必须要展示下我的文学功底了(其实是上高中抄别人作文学会的)–”古今之成大事业、大学问者,必经过三种之境界:”昨夜西风凋碧树。独上高楼,望尽天涯路。”此第一境也。”衣带渐宽终不悔,为伊消得人憔悴。”此第二境也。”众里寻他千百度,蓦然回首,那人却在灯火阑珊处。”此第三境也。此等语皆非大词人不能道。然遽以此意解释诸词,恐为晏欧诸公所不许也。” “
差不多就这意思,对事物的追求是逐渐加深的,当我们走到了深处,木然回首,一看,线性代数也就那么回事。
不扯没用的,继续说正交(orthogonality)
正交的三个层次是
- 向量正交
- 矩阵正交
- 子空间正交
两个向量正交是说他们的dot product为0
$$
v^tw=0 \,\, and \,\, ||v||^2+||w||^2=||v+w||^2
$$
前一个式子表明了位置关系,后面的距离表明了长度关系,当$v$和$w$是二维向量的话,这个也证明了平面勾股定理的正确性,当然,如果把勾股定理扩展到高维,也是成立的。
解释下垂直和正交的关系,垂直说的是相交直线间的角度关系,如果两个向量不想交,但是他们也可以有正交关系。
这里我们先略过矩阵正交,直接看子空间,因为矩阵正交在后面有个比较实用的分解
下面将要正式推出本文最最最重要的一个知识点,就是四个子空间的正交关系,子空间正交,就是说子空间A内的任意向量和子空间B内的所有向量全部互相正交。
definition:
$$
v^tw=0 \,\,for\,\,all\,\,v\,\,in\,\,V\,\,and\,\,all\,\,w\,\,in\,\,W
$$
这个条件看似挺严格,但是这个例子会让你豁然开朗:$Ax=0$ 这个是矩阵A的nullspace的表达,x属于nullspace,如果我们把A写的详细点($\dots a_i\dots$,表示矩阵中的一行),并且加入一个行向量 $r^t$(作用下面再说):
$$
r^tAx=r^t(Ax)=
r^t\begin{bmatrix}
\dots a_1\dots\\
\dots a_2\dots \\
\vdots\\
\dots a_n\dots
\end{bmatrix}
\begin{bmatrix}
x_1\\
x_2\\
\vdots\\
x_n
\end{bmatrix}=
r^t\begin{bmatrix}
0\\
0\\
\vdots\\
0
\end{bmatrix}
$$
所以
$$
r^tAx=0
$$
那么这说明了什么呢?$r^tA$是什么呢?同学们,这可是A的行空间啊,x是nullspace,他俩乘在一起是0啊,说明对于任意这两个空间的内的向量的dot product都是0啊,亲人们,正交啊。
上面的完整推到过程只用到了$Ax=0$这个事实,也就是规定x属于Nullspace的前提。
同样的道理可以推导出,列空间和左Nullspace也是正交的,那么我们就有另一个部分Fundamental Theorem了:
| Fundamental Theorem Part II(不完整版) |
|---|
| The row space is perpendicular to the nullspace |
| The column space is perpendicular to the nullspace of $A^T$ |
Fundamental Theorem I 说的是四个subspaces之间的维度的相互关系,第二部分说的是四个subspaces之间的正交关系,看来线性代数的核心是这四个subspace没错了。
正交互补(Orthogonal Complements)
This is very important ,The Fundamental subspace are more than just orthogonal in pairs.Their dimansions are also right.说实话,right这个词我想了半天也不知道对应中文那个词,三维空间中的两条线正交,但是他们并不可能是一个属于$3\times 3$矩阵的nullspace和rowspace因为他们都是dimension 1的加起来并不是3?你要问我为什么,往下看喽
Definition:Orthogonal Complement of a subspace V contains every vector that is perpendicular to V.This orthogonal subsapce is denot $V^{\perp}$(pronounced “V perp”)
通过上面的定义以及上面nullspace和rowspace正交的推到可以得出,row space的orthogonal Complement肯定是nullspace中所有vector,也就是说不存在一个向量,正交与rowspace却不属于nullspace。
证明非常日能够以,基本就是改改上面的那段推导。
反过来依然成立,如果以vector正交于nullspace,那么它一定属于rowspace,证明如下:
如果一个vector 正交于nullspace,而不属于rowspace,那么把vector添加到矩阵A最下一行形成A’,那么$A’x=0$依然成立,也就是说nullspace不会改变,但是rowspace却增加了(rank增加了1),那么$r+(n-r)=n$将不再成立,所以vector一定属于rowspace
各位,大招来了,本章,本书的重点:
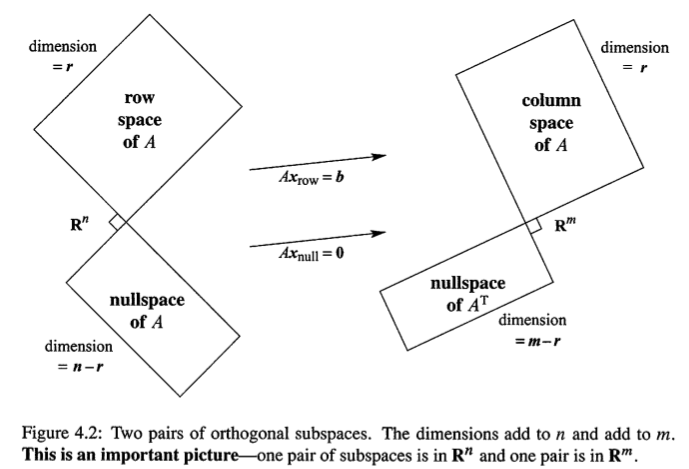
没错,就是之前上一张重点的图的一个信息补全,这里面值得注意的包括subspace之间的正交关系,以及dimension之间的互补关系,但要注意一下,其实在使用消元确定$Ax=b$解的时候可以得到nullsapce和columnspace之间的dimension互补关系,但是这里面把rowspace和nullspace写到一起主要还是正交的关系,而且向量长度相同n,加上rowspace和columnspace的dimension永远是一致的(rank),所以也就是这么放了(以上是我自己的理解)
| Fundamental Theorem Part II(完整版) |
|---|
| $N(A)$ is the orthogonal complement of the row space $C(A^T)$ (in $R^n$) |
| $N(A^T)$ is the orthogonal complement of the row space $C(A)$ (in $R^m$) |
解读:Fundamental Theorem Part I给出维度关系,Fundamental Theorem Part II给出垂直关系,complement时表示一个向量$x\,in\,R^n$总能分解到rowspace和nullspace两部分,而且根据两个subspace之间的dimension关系,可以确定,rowspace和nullspace加起来是完整的$R^n$空间(这个后面有讨论)
当$A(x_r+x_n)$时,奇迹出现了,还记得我们写Ax=b的无数个解的时候的完整解么?
$$ x=x_{particular}+x_n$$
和上面这种形式是对应的
矩阵A和向量相乘,可以有很多种解读,但是说到最根本的地方就是,$Ax$就是为了让x goes to column space,并没有其他什么更高级的功能。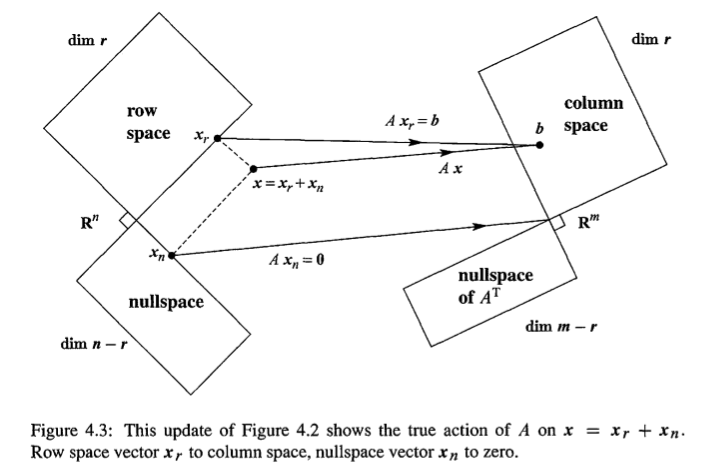
通过上面那张图可以看出,任何一个n维向量可以被分解到rowspace和nullspace,然后通过A goes to column space和 0
这里最重要的是任何一个属于$R^n$的向量都能被分解到row space 和 null space
下面是我的幡然悔悟的一个非常重要的问题,为什么不是每个矩阵都有逆:
来仔细观察箭头,$x_r$->$x_b$,是单射,没错,如果是单射就有逆运算,对于列空间的一个元素都有且只有一个行空间中的向量与之对应,但是由于不存在$A^{-1}$ 使得 $x_n=A^{-1}0$成立,也就是说不存在$A^{-1}$ 使得 $x=A^{-1}b$这也是为什么不是所有的矩阵都有逆,但是我们能确定一个 $\hat{A}^{-1}$ 使得 $x_r=\hat{A}^{-1}b$成立,这个戴帽子的A叫做pseudoinvers ,伪逆
这也告诉我并不是因为矩阵行列式为0他才没有逆,以前老师说,来算行列式,值是0矩阵没有逆,说的的确是真理,但是他一直也没说为啥。
组合子空间基
这段补充说明下矩阵基bases的一些扩展,主要还是用到上面那张图,就是离这里最近的那张带映射的图,rowspace和nullspace是可以span整个$R^n$的,比如在rowspace中找到r个线性独立的bases加上nullspace里面n-r个线性独立的bases,他们就能span出整个空间,为啥?因为这两个空间里的bases肯定线性独立,人家都正交了,哪来线性关系。所以,任何一个n维向量都能备份家到rowspace和nullspace,如果nullspace只有0向量,恭喜,$x=x_r$,A可逆,Ax=b有唯一解。在$R^n$ 中任何n个线性独立的vectors必然能span出$R^n$,反过来说也对,同理写成矩阵形式,一个由n个线性独立的向量组成的$n \times n$矩阵必然可逆。
注意:任何一个n维向量都能被split成一个rowspace中的向量和一个nullspace中的向量
总结
这篇内容实在是多到不行,而且都是精华,慢慢吸收,后面我如果发现问题可能还会补充,欢迎大家讨论
