Abstract: 关于正定矩阵的相关知识总结，正定矩阵在数学中的一个应用
Keywords: Positive Definite Matrices,Symmetric Matrices,Eigenvalues,Eigenvectors

正定矩阵

正定矩阵(Positive Definite Matrices)

正定矩阵，对这个矩阵印象深刻，知道学了这节以后，才知道，正定矩阵就是”Positive Definite Matrices-正的确定矩阵”，这个翻译也是耿直，

Positive Definite Matrices 定义为，对称矩阵，并且所有特征值全部大于0

那么我们第一个大问题就是如何确定一个矩阵是不是正定矩阵呢，求特征值肯定是根本方法，定义都说了，对称矩阵，特征值大于0，求出所有特征值，那么自然明朗了，但是有时候我们只需要知道是不是正定矩阵，而不需要知道特征值，这样的话计算代价有点大，我们需要找点别的招数，来避免求特征值。
接下来我们的目标是：

1. 找到能快速判断对称矩阵的特征值都是正数
2. 正定矩阵的重要应用

$2 \times 2$ 矩阵

对于 $A=\begin{bmatrix}a&b\\b&c\end{bmatrix}$ 什么情况下特征值是正的呢？因为只有两个特征值，那么我们考虑第一个条件：

1. 两个正数相乘，结果是正数

但是如果两个复数相乘也是复数，所以引入第二个条件：

2. 两个正数相加，结果是正数

那么如果满足，两个特征值相加是正数，相乘也是正数，那么肯定特征值全部都是正数。
又因为我们已知特征值相乘等于行列式，相加等于trace，那么：

$$a+c>0\\ and:\\ ac-b^2>0$$
就是$2 \times 2$ symmetric Matrices 正定的充分必要条件啦，当然还可以做个简化$ac-b^2>0$ 中如果 $a>0$ 和上面的式子等效：
$$a>0\\ and:\\ ac-b^2>0$$
注意关联词哦是and两个必须同时发作，那么这个条件才算是成功了.举两个计算的🌰。
$$A_1=\begin{bmatrix}1&2\\2&1\end{bmatrix}\;\;ac-b^2=1-4<0\\ A_2\begin{bmatrix}1&-2\newline -2&6\end{bmatrix}\;\;ac-b^2=6-4>0\;\;a=1>0$$
结论
$A_1$ 不是正定的
$A_2$ 是正定的

不定矩阵，正定矩阵，负定矩阵(Indefinite,Positive Definite and Negative Definite)

有正定就应该有负定，零正定（这个没有，0被分配到大于等于0的行列叫做半正定）或者不定矩阵。

1. Positive Definite：对称矩阵特征值全部为正数
2. Negative Definite：对称矩阵特征值全部为负数
3. Indefinite： 特征值有正有负，不定矩阵
4. Positive Semidefinite：对称矩阵，特征值大于等于0

正定也好不正定也好，我们可以现在想一想在空间上的操作到底是个什么鬼：
学习对称矩阵，我们一直在研究的是对角化，对角化作为一种分解方式和LU，QR等有着相同的身份，但是从书籍上的讲解篇幅和教授描述，都要比LU，QR更具体更深入，所以，对角化应该更有市场，我们接下来就从对角化来说说正定矩阵A:

$$A=S\Lambda S^{-1}\\ Q=S\\ A=Q\Lambda Q^{-1}$$
这个是上上上一篇讲述的，但是上一篇有一个惊天的秘密可以足够清晰的帮我们研究正定矩阵，也就是当对称矩阵A和一个向量相乘的时候，从空间的角度来讲，这个向量被投影到了A的列空间，但A的列空间和特征向量的空间不一致（特征向量可能比A的列向量维度大，因为当A存在0特征值的时候，相当于给自己降维了，也就是A是全体特征向量的子空间），那么现在:
$$u=c_1q_1+c_2q_2+\dots +c_nq_n=Qc\\ A=Q\Lambda Q^{-1}\\ Au=Q\Lambda Q^{-1}Qc=Q\Lambda (Q^{-1}Q)c=Q\Lambda (Q^{-1}Q)c=Q\Lambda c\\ Q\Lambda c= \begin{bmatrix}&&\\q_1&\dots &q_n\\&&\end{bmatrix} \begin{bmatrix}\lambda_1&&\\&\ddots &\\&&\lambda_n\end{bmatrix} \begin{bmatrix}c_1\\\vdots \\c_n\end{bmatrix}= c_1\lambda_1 q_1+\dots +c_n\lambda_n q_n$$
看到什么了？老铁们，一个向量乘以一个对称矩阵，相当于把这个向量以特征向量们为基，然后长度伸缩特征值倍，不改变方向且没有0的是正定矩阵，有0的是半正定，这时候有些方向上的长度被消灭了，也就是说向量分解到特征向量基空间少一维，也就是A并不是满空间的，也就是singular矩阵，和前面的0正好对应，如果有正有负，那就是瞎搞了，哈哈哈哈。
Negative Definite， Indefinite的🌰就不说了，后面会有一个section专门讲Positive Semidefinite。

能量基的定义 (Energy-based Definition)

能量based的定义，能量一般都是正的，所以这个和正定矩阵有关系也不那么令人惊讶，从源头看$Ax=\lambda x$ 是一个矩阵的特征值和特征向量，如果我们在这两边同时乘上点什么：

$$x^TAx=x^T\lambda x=\lambda x^Tx\\ x^Tx=|x|^2 \geq 0$$
特征向量都是非零向量所以上面等号在特征向量前提下永不成立，那么也就是只要保证 $x^TAx>0$ 那么就有 $\lambda >0$ 得出矩阵可能是正定的，然后检验所有特征向量，这个工作量也有点大，根据其他一些应用，这里提出一个新的定义，关于能量的$x^TAx$ 表示一个系统的能量，其必须大于0.也就是说对于一个矩阵，其能量为正，这个矩阵定义为正定矩阵。
上面这个是定义正定矩阵的一个方法，也就是说了一个有点实际意义的定义，而不是上来拿枪指着你，说，“小子，特征值大于0的对称矩阵就是正定矩阵，说不行打死你”，所以这种定义在应用中出现的时候，要想到正定矩阵就好。
上一篇有一块介绍pivot和Eigenvalue之间的关系，他们的符号是相同的，也可以测试$x^TAx$是正是负。

Definition: A is positive definite if $x^TAx>0$ for every nonzero vector x:

$$x^TAx= \begin{bmatrix}x&y\end{bmatrix} \begin{bmatrix}a&b\\b&c\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}=ax^2+2bxy+cy^2>0$$

这个就是能量观点下定义的完整写法，如果理解了这个过程也就对这个形式没什么困惑了，我记得我之前是老师说，来，把这个公式记住。。。
$ax^2+2bxy+cy^2$ 是一个碗的形状，当然xy都不是零的时候。

根据能量观点可以得到正定矩阵的可加性，也就是规模相同的两个正定矩阵，相加也是正定的，证明过程如下，假设其中A，B规模相同，切都是正定的：

$$C=A+B\\ x^TAx>0\\ x^TBx>0\\ x^T(Ax+Bx)=x^T(A+B)x=x^TCx>0$$
QED

$R^TR$

这是一种新的判断正定的方法，通过上面能量的观点$x^TAx$ 延伸，出如果能把A分解成一个矩阵和矩阵的转置相乘的形式，那么就能得到 $(Rx)^T(Rx)$ 的形式 那么这个形式下，如果$Rx\neq 0$ 必然其结果大于0（$Rx$ 是一个向量，所以 $(Rx)^T(Rx)$ 就变成了 $|Rx|$ 是一个长度）那么如果我们假设必然存在R，那么R要满足什么条件呢？ $Rx\neq 0$ 就是条件，对于所有非0向量，也就是R的Nullspace只有0向量，也就是R的列必须相互独立,这也是唯一的条件，如果矩阵能分解成$A=R^TR$ 的形式，R的列线性独立，那么A正定。
反过来也是正确的，如果矩阵R各列线性独立，那么 $A=R^TR$ A是正定矩阵。

正定矩阵”五项原则”

总结下我们判断正定的几种方法，他们互相等效，一个成立便可以推出其他所有：

1. All n pivots are Positive
2. All n upper left determinants are positive
3. All n Eigenvalues are Positive
4. $x^TAx$ is positive except at $x=0$ This is the energy-based Definition
5. A equal $R^TR$ for a Matrix R with independent columns

上面的2我们好像没有证明，左上角的行列式的值总和左上角矩阵的pivot有关系，如果第一个行列式为正(也就是1x1的矩阵，即第一个pivot为正)那么第二个矩阵（2x2）的行列式也为正的话，可以得出第二个pivot也是正的，以此类推，就能得到第一条，所有pivot都是正数，这个可以参考行列式文章Permutation 可以有些启发。

上面的五条基本上可以把线性代数大部分东西全包括进去了，消元，特征值，行列式，子空间，这些都要知道后，才能对上面的五条不存在疑惑，所以直接看本文的同学，不懂往回看。

从正定返回$R^TR$

我们回忆一下最初的分解形式$A=LDU$ 分解 当A是正定矩阵的时候，我们可以得到 $U=L^T$
所以$A=LDL^T$ 其中D是对角矩阵，如果给D开个根号是不是很完美，那么前提是D中所有元素都是正的（也就是所有pivots和Eigenvalue都是正的，这里两个概念等价）正定矩阵满足你的需求，所以就可以分解出来：

$$A=L\sqrt{D}(\sqrt{D}L)^T$$
上面这个是Cholesky Factor，针对正定矩阵的一种分解

半正定矩阵 (Positive Semidefinite Matrices)

如果特征值中包含0 ，那么 $x^TAx$ (x是特征向量) 有可能是0，也就是没有能量。并且写成 $R^TR$的形式。R总是有线性相关的列，具体原因看上面的证明自明，也就是奇异矩阵必然不是正定矩阵，但是可以使半正定矩阵，这个结论还是很欣慰的，并没有把奇异矩阵一棒子打死。
扩展x为任意变量的时候$x^TAx\geq 0$ 只有当x为对应于特征值为0的特征向量的时候等号成立。

一个应用（First Application: The Ellipse) $ax^2+2bxy+cy^2=1$

学习线性代数，从向量开始，我就有一种感觉就是线性代数当矩阵维度是2或者3的时候，应该是和几何有关系的，也就是我们能画出来的这些形状有关而不仅仅是解方程这么简单，线性变换，对图形的作用应该是比较直观的，所以我们来看书上的🌰，关于特征值，特征向量，以及椭圆的：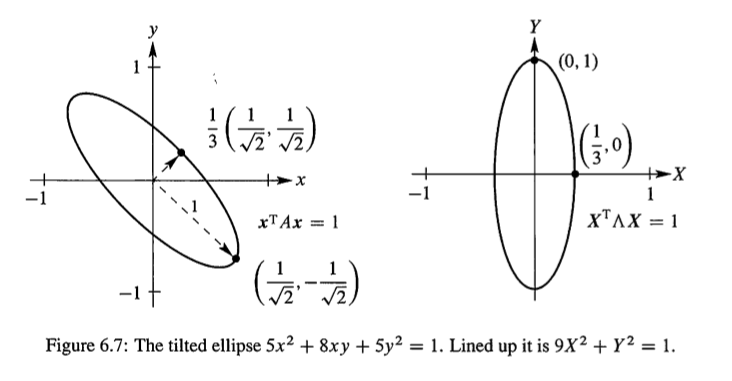

两个椭圆，一个倾斜的，一个立正的,两幅图能够看出下面这些信息：

1. The tilted ellipse is associated with A. Its equation is $x^TAx=1$
2. The lined-up ellipse is associated with $\Lambda$ .Its equation is $x^T\Lambda x=1$
3. The rotation matrix that lines up the ellipse is the eigenvector matrix Q

第一个歪的椭圆的方程是：

$$\begin{bmatrix}x&y\end{bmatrix} \begin{bmatrix}5&4\\4&5\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}=1\\ A=\begin{bmatrix}5&4\\4&5\end{bmatrix}\\ \lambda_1=9\\ \lambda_2=1\\ x_1=\begin{bmatrix}1\\1\end{bmatrix}\\ x_2=\begin{bmatrix}1\newline -1\end{bmatrix}$$
分解成
$$A=Q\Lambda Q^T= \frac{1}{\sqrt{2}}\begin{bmatrix}1&1\\1&-1\end{bmatrix} \begin{bmatrix}9&0\\0&1\end{bmatrix} \frac{1}{\sqrt{2}}\begin{bmatrix}1&1\\1&-1\end{bmatrix}$$
然后把xy弄进去
$$\begin{bmatrix}x&y\end{bmatrix} Q\Lambda Q^T \begin{bmatrix}x\\y\end{bmatrix}= \frac{1}{\sqrt{2}} \begin{bmatrix}x&y\end{bmatrix} \begin{bmatrix}1&1\\1&-1\end{bmatrix} \begin{bmatrix}9&0\\0&1\end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix}1&1\\1&-1\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\\ = \frac{1}{\sqrt{2}} \begin{bmatrix}x&y\end{bmatrix} \begin{bmatrix}1&1\\1&-1\end{bmatrix} \begin{bmatrix}9&0\\0&0\end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix}1&1\\1&-1\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\\ + \frac{1}{\sqrt{2}} \begin{bmatrix}x&y\end{bmatrix} \begin{bmatrix}1&1\\1&-1\end{bmatrix} \begin{bmatrix}0&0\\0&1\end{bmatrix} \frac{1}{\sqrt{2}} \begin{bmatrix}1&1\\1&-1\end{bmatrix} \begin{bmatrix}x\\y\end{bmatrix}\\ = 9(\frac{x+y}{\sqrt{2}})^2+1(\frac{x-y}{\sqrt{2}})^2$$

最后一步矩阵计算比较长，这里省略了，中间没有trick，我把分解那步写出来也是为了好看，，结论是正确的，观察上面结果，两个系数居然是特征值，厉害不？不是pivot也不是别人，而是特征值，在两个平方内部，是两组向量 $(1,1)$ 和 $(1,-1)$ 这个是特征向量，也是椭圆轴的方向，所以当矩阵扩展到多维的时候（还是正定矩阵），的时候所有特征向量是这个超椭圆的所有轴，这也是为什么叫主轴定理的原因啦，不光是主轴，特征值还能表示在主轴方向上的长度，这个也很值得重视，因为方向和长度是向量的两个组成因素。
进一步，我们看看怎么把歪着的椭圆立起来

$$X=\frac{x+y}{\sqrt{2}}\\ Y=\frac{x-y}{\sqrt{2}}\\ for:\\ 9(\frac{x+y}{\sqrt{2}})^2+1(\frac{x-y}{\sqrt{2}})^2\\ get:\\ 9X^2+Y^2=1$$
那么X最大值是 $\frac{1}{3}$ ,Y 最大值是 $1$ 这两个值的得到方法都是 $\frac{1}{\sqrt{\lambda}}$ 从图上也能看出来，长轴是1对应小的特征值，短轴是$\frac{1}{3}$ 对应长的特征值。
在xy中，轴的方向沿着A特征向量方向，在XY中是 $\Lambda$ 的特征向量，也就是坐标轴了，数值上看是这样的，从原理上：

$$\begin{bmatrix}x&y\end{bmatrix} Q\Lambda Q^T \begin{bmatrix}x\\y\end{bmatrix} =\begin{bmatrix}X&Y\end{bmatrix} \Lambda \begin{bmatrix}X\\Y\end{bmatrix}= \lambda_1X^2+\lambda_2Y^2=1$$
xy可以表示一个被线性变换后的坐标表示，当这个坐标被Q投影了以后，就变成了图中正的图形了，可以观察特征值决定了椭圆有多椭，当特征值都是1的时候也就是 $\Lambda =I$ 的时候，这个图形就是个圆，如果有负数特征值，那就变成双曲线了，如果都是负的。。这个我也不知道是啥了（就有虚数部分了，这个我还不懂）

Conclusion

本文主要讲解正定矩阵，最后的应用是最精彩的部分，前面主要是线性代数知识点的大串讲，可能有些不那么详细，大家可以自己再补充一些，到这里线性代数高潮部分已经完成了一大半，完成了下面就是相似矩阵和svd，线性代数基础部分也就算是快结束了，待续。。