Abstract: 本文介绍正态分布的数学性质
Keywords: The Normal Distributions
正态分布
一共要写四篇,哪来那么多废话。
首先我们要从最基础的原始的正态分布的数学原理说起
正态分布的性质 Properties of Normal Distributions
正态分布的定义 Definition
到目前为止,我们还没看到正态分布长什么样。
Definition and p.d.f. A random X has the normal distribution with mean $\mu$ and variance $\sigma^2$ ($-\infty<\mu<\infty$ and $\sigma > 0$) if X has a contimuous distribution with the following p.d.f.
$$
f(x|\mu,\sigma^2)=\frac{1}{(2\pi)^{\frac{1}{2}}\sigma}e^{-\frac{1}{2}(\frac{(x-\mu)}{\sigma})^2}\text{for} -\infty<x<\infty
$$
定义对于我们来说就是个准确的命名过程。那么我们接下来要证明的是定义里说的对不对?
Theorem $f(x|\mu,\sigma^2)=\frac{1}{(2\pi)^{\frac{1}{2}}\sigma}e^{-\frac{1}{2}(\frac{(x-\mu)}{\sigma})^2}\text{for} -\infty < x< \infty$ is a p.d.f.
思路:证明一个表达式是不是,p.d.f.,肯定要根据p.d.f.的定义,①不能出现负数,②积分结果是1。
首先观察函数,发现其不可能出现负数,所以性质1符合p.d.f.的性质
那么接下来是求积分,并确保是1,不是说不能积分么,这里怎么做呢?
首先我们令 $y=\frac{x-\mu}{\sigma}$ 那么
$$
\int^{\infty}_{-\infty}f(x|\mu,\sigma^2)dx=\int^{\infty}_{-\infty}\frac{1}{(2\pi)^{1/2}}e^{-\frac{1}{2}y^2}dy\\
\text{we shall now let:}\\
I=\int^{\infty}_{-\infty}e^{-\frac{1}{2}y^2}dy
$$
所以我们只要证明 $I=(2\pi)^{1/2}$ 就算是得到结论了,但是怎么证明呢?我们用用1的特点吧,1和1相乘还是1所以我们让两个积分相乘,我们来到了二重积分的世界解决这个问题:
$$
\begin {aligned}
I^2&=I\times I=\int^{\infty}_{-\infty}e^{-\frac{1}{2}y^2}dy \cdot \int^{\infty}_{-\infty}e^{-\frac{1}{2}z^2}dz\\
&=\int^{\infty}_{-\infty} \int^{\infty}_{-\infty}e^{-\frac{1}{2}(y^2+z^2)}dydz\\
\text{to the polar coordinates } r \text{ and } \theta :\\
I^2&=\int^{2\pi}_{0} \int^{\infty}_{0}e^{-\frac{1}{2}(r^2)}rdrd\theta \\
\text{substitute }v=r^2/2\\
&\int^{\infty}_{0}e^{-v}dv=1
\end{aligned}
$$
证毕。
也就证明了两个这个积分相乘的结果是1,但是我们并没有求出他的反函数。
正态分布的距生成函数 m.g.f.
m.g.f. 一旦得到相应的均值和方差就非常简单了。
Theorem Moment Generating Function.The m.g.f. of the distribution with p.d.f. given by upside is
$$
\begin{aligned}
\psi(t)&=e^{\mu t+\frac{1}{2}\sigma^2t^2}&\text{ for }-\infty<t<\infty
\end{aligned}
$$
证明上面定理的唯一办法就是我们求一下正态分布定义中那个p.d.f.的m.g.f.看结果是否一致。
$$
\begin{aligned}
\psi(t)&=E(e^{tX})=\int^{\infty}_{-\infty}\frac{1}{(2\pi)^{1/2}}e^{tx-\frac{(x-\mu)^2}{2\sigma^2}}dx\\
\text{square inside the brackets:}\\
tx-\frac{(x-\mu)^2}{2\sigma^2}&=\mu t+\frac{1}{2}\sigma^2t^2-\frac{[x-(\mu+\sigma^2t)]^2}{2\sigma^2}\\
\text{Therefore:}\\
\psi(t)&=Ce^{\mu t+\frac{1}{2}\sigma^2t^2}\\
\text{where: }\\
C&=\int^{\infty}_{-\infty}\frac{1}{(2\pi)^{1/2}\sigma}e^{-\frac{[x-(\mu+\sigma^2t)]^2}{2\sigma^2}}dx
\end{aligned}
$$
然后我们用 $\mu+\sigma^2t$ 替换掉 $\mu$ 并且 $C=1$ 因此证明了结论的正确性
证毕。
思路是按照m.g.f.的定义,然后把里面的凑成正态分布的样子利用积分为1,化简表达式
正态分布的均值和方差 Mean and Variance
Theorem Mean and Variance.The mean and variance of the distribution with p.d.f. given by definition upside are $\mu$ and $\sigma^2$ ,repectively.
证明方法就是直接用m.g.f.求导就可以了:
$$
\begin{aligned}
\psi’(t)&=(\mu+\sigma^2t)e^{\mu t+\frac{1}{2}\sigma^2t^2}\\
\psi’’(t)&=([\mu+\sigma^2t]^2+\sigma^2)e^{\mu t +\frac{1}{2}\sigma^2t^2}\\
\text{Plugging } t=0\\
E(X)&=\psi’(0)=\mu \\
Var(X)&=\psi’’(0)-[\psi’(0)]^2=\sigma^2
\end{aligned}
$$
注意m.g.f.对于所有 $t$ 都有限,所以所有正态分布的距都存在。
正态分布的形状 the Shapes of Normal Distribution
我们上面稀稀拉拉写了一些常见的性质,但是到现在我们还不知道正态分布长什么样呢?
分析p.d.f和我们已经计算出来的数字特征,我们可以总结出下面这些基本信息:
- 均值和中值都是 $\mu$
- $f(x|\mu,\sigma^2)$ 在 $x=\mu$ 时得到最大值。
- 二次求导后在 $\mu \pm \sigma$ 处为0,为曲线拐点。
于是我们会得到钟形曲线:
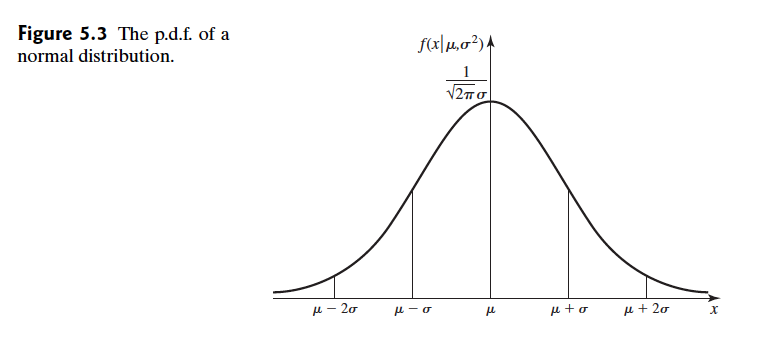
并不是所有钟形曲线都是正态分布家族的,比如前面介绍的不存在期望的柯西分布,他的尾巴跟我们的正态分布不太一致。
线性变换 Linear Transformations
我们接着研究研究正态分布的线性变换。
Theorem If $X$ has the normal distribution with mean $\mu$ and variance $\sigma^2$ and if $Y =aX+b$ ,where $a$ and $b$ are given constants and $a \neq 0$ ,then $Y$ has the normal distribution with mean $a\mu+b$ and variance $a^2\sigma^2$ .
定理给出了正态分布对应的随机变量经过线性变换后的结果,我们来计算下,证明定理的正确性。
证明:
使用m.g.f ,我们来计算 $\psi_Y$
$$
\psi_Y(t)=e^{bt}\psi(at)=e^{(a\mu+b)t+\frac{1}{2}a^2\sigma^2t^2} \text{ for }-\infty <t<\infty
$$
比较正态分布的m.g.f
$$
\begin{aligned}
\psi(t)&=e^{\mu t+\frac{1}{2}\sigma^2t^2}&\text{ for }-\infty<t<\infty
\end{aligned}
$$
可以看出线性变化后的分布是一个均值为 $a\mu+b$ 方差为 $a^2\sigma^2$ 那么我们得到一个新的正态分布,并且新正态分布的参数和原正态分布有关系
总结
本文主要介绍正态分布的数学性质。后面我们继续研究标准正态分布和对数正态分布。
待续。。。
