Abstract: 本文继续上文的离散随机变量的观点,将部分试验模型转换到连续随机变量的观点上。
Keywords: Continuous Random Variable,Continuous Distributions,Probability Desity Function,Uniform Distributions on Intervals
连续分布
今天的废话想说说关于转行,之前去看中医(别问我信不信中医,学过概率的人都应该有自己的模型去评估一件事)那位老师真的是白发苍苍,很有医者风范,甚是慈祥有条不紊,在询问病情的过程中无意中聊到现在各行业的发展,老人家说,现在有些人两年三年就换个行业,还说叫什么转型,这么换来换去的什么东西能做好?一边说甚至有点义愤填膺的感觉。
其实我之前也有这种感觉,为啥这个人先是云计算,然后又去智能穿戴了,后来又智能家居,然后3D打印,后来就人工智能了,问问没准最近可能在研究区块链了,更让人感慨的是,他们研究个三五个月就敢自称专家了,如果有个博士学位,或者大公司平台背书,那整个过程能更加自然流畅。
我一直在对自己身边的人宣传要做自己喜欢的事。但是如果你喜欢的事经常变,而且是啥新鲜变成啥,那我只能说甚是与时俱进。
为啥我要回到数学,一篇一篇的写博客,做练习,我觉得我之前也太激进了,就像一个三岁小孩就急着上战场,手枪还用不好呢,就想用M416,太扯淡了,拿着枪照镜子觉得很有自信,当真要你死我活的时候,估计会死的很难看,当然不是最惨的,旁边那个两岁的拿着AK跟某组织正在申请高新技术企业呢!
概率密度函数 The Probability Density Function
继续我们的概率论,首先我们回忆一下,我们首先从试验开始,然后得到样本空间,每个试验结果都是一个样本点,对应一个概率,试验结果的个数是离散的,确定的,比如扔硬币,扔骰子,随后我们将这些结果通过一个函数映射到一个随机变量,使其更加数学化,随机变量是个函数,有时候也表示函数值,为了研究这个函数值对应的概率,我们又提出了distribution这个概念。今天我们将随机变量这个坑补齐,因为我们研究离散的随机变量时,其定义域和值域都有洞,我们今天把洞补齐。
学过数学分析,或者是研究过实数系的同学都知道,自然数,整数,有理数(比例数)这些数都是不连续的,因为有洞,这些洞比如 $\sqrt{2}$ 这个位置,就是有理数没办法表示,后来我们为了补全整根数轴,我们得到了实数系,这个没有洞的数,那么我们今天就是想找个试验,能把实验结果映射到一段连续的实数上(可以是有界的也可以是无界的),然后研究他的性质。
在研究连续随机变量前,我们可以引进一个关于面积的模型,其实书上很早之前就有,一般的概率论书上一般在古典概率部分就会提出这个面积模型。
举个🌰 :
我们有一家工厂,每个月用水是在 $[10,110]$ 吨,用电在 $[100,1100]$ 千瓦时,并且是完全随机的均匀的,那么我们可以计算用水在 $[20,40]$ 吨,用电在 $[600,800]$ 千瓦时的概率是多少?
这里我们可以画一个图: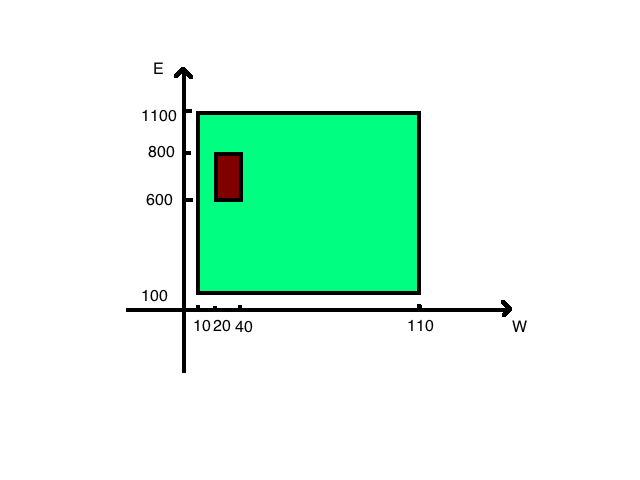
从直觉上来说,中间这小块的面积与完整面积的比例就应该是上面描述的事件的概率。
从频率的角度上来说也是,因为每个点出现的可能性相同。那么一个区域出现的可能性就是这个区域的积分,积分在几何的表示是面积,那么我们用面积比来近似概率应该没有问题,那么,我们如果是这个思想继续展开,一个点的概率是多少呢?点没有面积,所以每个点的概率是0,而我们之前认为事件的概率是0,表明事件不可能发生,但是在这个例子里面,任何一个点都有可能发生,矛盾了,那么我们的模型有问题?还是前面的公理有问题?我们接着往下看。
我们发现我们认为事件概率是0的事件不可能发生的事件是离散的,也就是事件数量是有限的,而我们这个例子的事件个数是无限多的,那么我们要从连续的角度重新思考事件,随机变量和对应的概率的问题了。
连续分布,连续随机变量 Continuous Distribution & Continuous Random Variable
Definition Continuous Distribution/Random Variable: We say that a random variable $X$ has a continuous distribution variable if there exists a nonnegative function $f$ ,defined on the real line,such taht for every interval of real nombers (bounded or unbounded),the probability that $X$ takes a value in the interval is the integral of $f$ over the interval
我们定义下连续分布和连续随机变量(依然是个函数),定义连续随机变量(函数),在实数轴上,每一个区间(有界或者无界)对应的概率是这个区间上 $f$ 的积分。
$$
Pr(a\leq X\leq b)=\int^b_af(x)dx
$$
上面这个定义和上面的例子相互对应,所以,上面的例子的解法没有问题,那么为什么单点概率会是0?因为当事件的随机变量产生的结果是连续的,那么无数个事件对应无数个连续的随即变量值,为了满足公理 Kolmogorov Axiom 3 这些事件的概率和必然是1,那么,只有通过积分,才能把无数个小到零的数字,加到1,所以连续随机变量的值,描述要用到积分。又因为单点积分没有定义(用黎曼积分没办法算),所以我们可以理解,上面的定义是很有道理的。计算一个区间内的随机变量的积分,比如 $[x-\epsilon,x+\epsilon]\text{ for }(\epsilon>0)$ 上的积分,来近似表示x处的概率,当 $\epsilon \to 0$ 可以完成这个近似。
总结起来就是:连续事件有无穷多个随机变量值,那么单个随机变量值变得毫无意义(无限趋近于0),只有用(某区间上的)无数多个随机变量的概率的积分( $>0$ ),与完整样本空间上的随机变量概率的积分和(1)的比例来描述这部分(区间上的)的概率。
那么上面这个表达的一个突出结果就是 $f$ 将会是非常重要的,这个$f$ 有点像离散随机变量的概率函数,但是操作起来又有很大差别。
概率密度函数的定义 Definition Probability Density Function/p.d.f/Support
Definition Probability Density Function/p.d.f/Support:If $X$ has a continuous distribution ,the function $f$ described in definition Continuous Distribution/Random Variable is called the probability density function(abbreviated p.d.f)of $X$.The closure of the set ${x:f(x)>0}$ is called the support of (the distribution of) $X$
上面关于连续随机变量的定义中 $f$ 的定义并不是随意的,而且这个 $f$ 可以算是一节大佬了,因为后面很多连续随机变量都要用它表达,被称为概率密度函数,过程简称pdf,这个函数能够表征一个连续随机变量的分布请款个,与离散情况下的概率函数功能相似,而且性质也类似,每个连续试验可以对应不同的pdf(可以移植上文中概率函数的证明方法),并且我们能够得到一个关于support(支撑) 的定义,连续随机变量所在的闭区间必须要能保证pdf大于0(因为有等于0的情况),这个区间就是一个support。
图解的话就是下面的图了: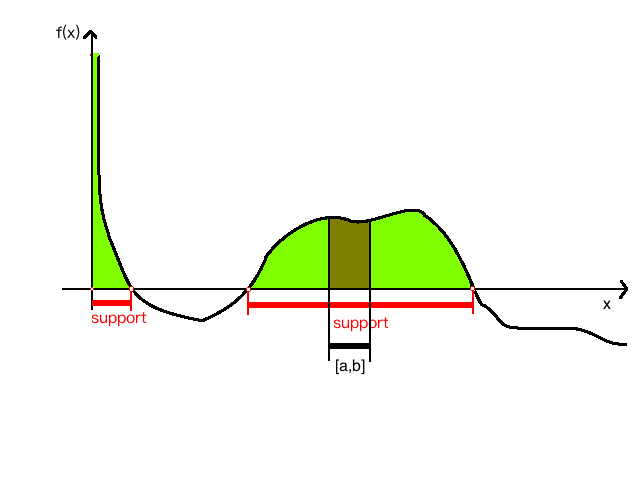
图中所有有定义的区间(绿色)的积分的和是1,指定区间的积分是映射到这个区间上的所有事件之一发生的概率。红色开区间是上面定义的support。上图描述了一个随机变量在两个分开的区间上的pdf。
所以pdf就是连续随机变量的一种描述方式,后面还有别的描述方式,但是pdf特殊就特殊在,连续随机变量是用它来定义的。
pdf需要满足以下两点性质:
性质一:
$$
f(x)\geq 0 \quad \text{for all } x
$$
性质二:
$$
\int^\infty_{-\infty}f(x)=1
$$
性质一和性质二都是为了满足柯氏公理而产生的,大于等于0表示不可能出现负数的概率,积分等于保证公理三成立。
还是要强调,连续随机变量的概率密度函数(p.d.f.)中概率等于0,事件不可能发生。
概率(密度)函数的不唯一性 Nonuniqueness of the p.d.f.
和前面所说的概率函数不“唯一”一样,pdf也不唯一,一个原因是关于随机变量(函数)的选择问题,还有很重要的一点,由于单点pdf对于整体而言其概率是0,那么其pdf值可以为任意值,而保持任意包含此点的区间上的pdf积分值不变(也就是概率不变)。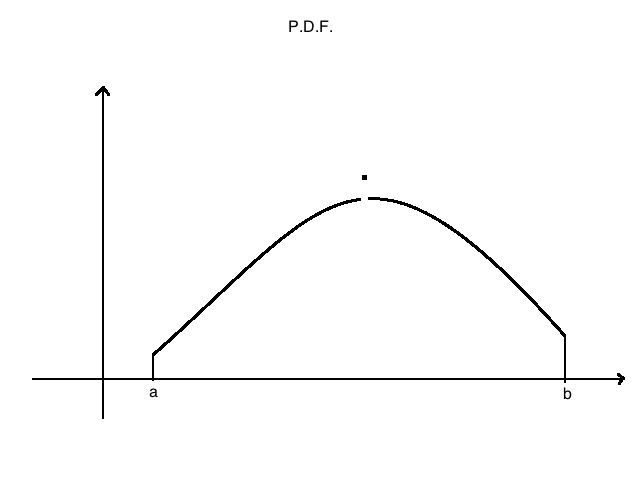
这个pdf和下面这个pdf等效,但是却不一致:
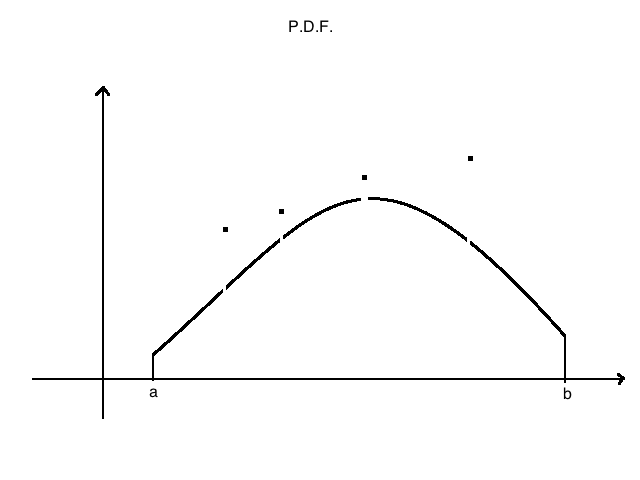
所以每个连续随机变量都有无穷个pdf,我们通常会选取最自然的那个,而且尽量不要用这些存在间断点的pdf,因为从函数研究的角度来讲,这个将会很麻烦,我们把事件过渡到实数域的目的就是为了利用数学工具,比如函数,积分,微分等,如果还人为的引入障碍就有点不明智了,但是如果引入间断点可以更好的表述模型,那么也未尝不可。
还有一个要注意下,我们说过几种分布了,不如二项分布,伯努利分布,均匀分布,这些分布里面的分布,与连续分布,离散分布不是一回事儿:
区间上的均匀分布 Uniform Distributions on Intervals
我们扩展一下上一篇中的均匀分布,从离散扩展到连续,我们学习概率分布都是从均匀分布开始的,说明其具有非常简单的性质,当然,就是扔骰子嘛!
Definition Uniform Distribution on an interval:Let $a$ and $b$ be two given real numbers such that $a<b$.Let $X$ be a random variable such that it is known that $a\leq X \leq b$ and ,for every subinterval of $[a,b]$ ,the probability that $X$ will belong to that subinterval is proportional to the length of that subinterval .We then say that the random variable X has the uniform distribution on the interval $[a,b]$
翻译:一个区间上 $[a,b]$ 上任意一个区间上的概率(pdf的积分)等于这段区间的长度与整个定义区间的比例,那么这个分布就叫做在 $[a,b]$ 上的均匀分布(有些细节没有添加,可以从上面英文的定义找到)
所以根据上述定义,我们可以猜测也可以计算出,下面这个pdf是 $[a,b]$ 上的均匀分布的一个pdf。
Theorem Uniform Distribution p.d.f. If X has the uniform distribution on an interval $[a,b]$,then the p.d.f. of X is:
$$
f(x)=
\begin{cases}
\frac{1}{b-a} \quad \text{for} a\leq x\leq b\\
0\quad\quad \text{otherwise}
\end{cases}
$$
证明思路就是首先证明在所有可能的随机变量上其积分是1,这个结论是显而易见的。因为在区间外的任意区间上的积分都要是0,又可知在上述式子中,
$$
\frac{\int^{x_2}_{x_1}f(x)dx}{\int^{b}_{a}f(x)dx}=\frac{|x_2-x_1|}{b-a}\quad \text{for:} x_2>x_1
$$
恒成立,那么上述的p.d.f是均匀分布的p.d.f.之一。
QED
请注意:p.d.f对应值没有实际意义,这点与概率函数有着非常大的差异,p.d.f的值可以大于1,甚至可以是 $+\infty$ ,因为上面我们也看到了,pdf的区间积分才是表达概率的,所以概率的一些表要性质不需要pdf表现出来,而是需要pdf的区间积分表现出来。
举个例子:
计算下面pdf的概率:
$$
f(x)=
\begin{cases}
\frac{x}{8}\quad \text{for} 0<x<4\\
0\quad \quad \text{otherwise}
\end{cases}
$$
计算 $Pr(1\leq X \leq 2)$ 和 $Pr(X>2)$ :
$$
Pr(1\leq X\leq 2)=\int^2_1\frac{1}{8}xdx=\frac{3}{16}
$$
以及
$$
Pr(X>2)=\int^4_2\frac{1}{8}xdx=\frac{3}{4}
$$
混合分布 Mixed Distribution
混合分布这里简单介绍一下,当一个试验被二维随机变量映射时,将会产生一个二维的随机变量值这个值有两个维度,这两个维度相互之间可以有影响也可以没有影响,但是他们连续与否是完全独立的,也就是说两个输出值,其中一个是连续的,另一个离散的,这完全没问题,而具体的计算也可以分别参考离散和连续随机变量。
总结
本文主要讲如何用pdf来描述一个随机变量(值)的连续分布,后面我们继续研究连续情况下的分布表述,以及其他一些工具。
