Abstract: 本文介绍中心极限定理
Keywords: The Central Limit Theorem,The Normal distribution,The Delta Method
中心极限定理
读书的一个重要用途就是建立自己对事情的理解方法,在数学领域,尤其是概率和数理统计,学习这两门课程,可以让你对世界上所有的事情的理解改变一个角度,甚至统计最后可以解释哲学,那么这样解释自然的三种方法——神学,哲学,科学,就会被改成“神学”和“科学”了,如果哪天神学也被建模了,哈哈哈,世界大一统,这里并不是对宗教或者哲学家的任何不尊重,只是谈一个小想法😆
概率论快接近尾声了,本文讲完基本也就剩下一篇了,学了微积分,学了线性代数,学了数学分析,学了概率论,但是感觉自己还是没什么长进,这就是数学基础的困难,变现速度慢,但是作为长久投资,我相信是值得的。
本文我们介绍中心极限定理,上一篇的大数定理,围绕的一个核心观点就是,样本均值概率极限是分布均值。而今天的中心极限定理是描述样本均值的分布的。一个数量足够多的随机变量样本的样本期望(Sample Mean,一个随机变量)的期望是 $\mu$ 以及有限的方差 $\sigma^2$ 那么他的分布近似于均值为 $\mu$ 方差为 $\sigma^2/n$ 的正态分布。这个结论可以帮助证明正态分布可以用来建模一些随机变量,当然这些随机变量是多个独立的部分组成的。
我们本文会提出Delta方法来帮助我们一组随机变量样本的期望的函数变化后产生的新随机变量。
中心极限定理和大数定理放在后面是有目的的,因为我们马上要过渡到数理统计,而前面我们说了,我们的主要应用时根据数据(已知样本)找模型,也就是我们在数理统计里面要研究的,而中心极限定理和大数定理给出的就是样本和模型之间的理论关系。
中心极限定理 Statement of the Theorem
先举个🌰 :
临床试验,100个患者将接受治疗,患者有 0.5的可能性接受治疗,而其本人不知道自己是否接受治疗,我们这里假设所有患者之间相互独立,本实验的目的是观察新的治疗能否提高患者的治愈率,随机变量 $X$ 表示 100 个人中治愈的人数,如果接受治疗的治愈率是0.5和没有接受治疗治愈率的一样,那么 $X$ 就是 $n=100,p=0.5$ 的二项分布,那么根据二项分布的随机变量的数值,可以描绘出如下的图片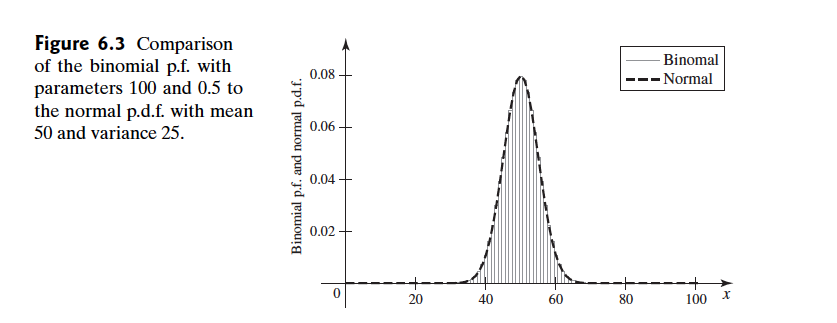
如果我们绘制一个均值为 $\mu=50$ 方差为 $\sigma^2=25$ 的正态分布,刚好可以把这个二项分布包裹起来
在Poisson分布的学习中,当我们遇到 $n$ 很大 $p$ 很小,而$np$ 有不大不小(这个标准有点含糊) 的时候可以用泊松分布来近似二项分布,上面的例子我们看出,当 $n$ 很大而 $p$ 又不太小的时候,正态分布可以用来近似二项分布。
中心极限定理就是一个形式化的描述,来描述正态分布是如何近似i.i.d的随机变量的一般和(随机变量)或者均值(样本均值,随机变量)的分布的。
在正态分布的那一课证明了 $n$ 个独立同正态分布的的随机变量,如果其分布均值是 $\mu$ 分布方差是 $\sigma^2$ 那么样本均值 $\bar{X}_n$ 也是正态分布,均值是 $\mu$ 方差是 $\sigma^2/n$ 而我们本篇就会介绍根据中心极限定理,无论原始分布是否是正态分布,其样本均值分布都可以用正态分布来近似,样本均值。
而对于样本是独立的不同分布的随机变量的话,我们也有一套中心极限定理能够建模这些样本的和。
注意,中心极限定理,有两个版本,就像微积分基本定理有两个一样,中心极限定理,一个针对独立同分布的样本,一个针对独立不同分布的样本,大家要注意区分。
首先来看同分布的,这个定理由 Lindeberg 和Levy 在1920s初期证明:
Theorem Central Limit Theorem(Lindeberg and Levy) If the random variables $X_1,\dots,X_n$ form a random sample of size $n$ from a given distribution with mean $\mu$ and variance $\sigma^2$ ( $0<\sigma^2<\infty$ ) ,then for each fixed number $x$ ,
$$
lim_{n\to \infty}Pr[\frac{\bar{X}_n-\mu}{\frac{\sigma}{n^{1/2}}}\leq x]=\Phi(x)
$$
where $\Phi$ denotes the c.d.f. of the standard normal distribution.
书上并没有给出上述定理的证明,而是给出了定义的解释说明(我觉得还是证明了的定理用的踏实,但是有些定理证明过于复杂,所以理解定理含义,也算是站在巨人的肩膀上,但还是证明一下用的踏实。),定理说明是,从任何一个分布中选取大量的随机变量,这个分布的均值是 $\mu$ 方差是 $\sigma^2$ 不需要考虑这个分布式离散的还是连续的,则 $n^{1/2}(\bar{X}_n-\mu)/\sigma$ 近似于标准正太分布;那么根据正态分布的性质,样本均值 $\bar{X}$ 近似于 $\mu_{\bar{X}}=\mu,\sigma^2_{\bar{X}}=\sigma^2/n$ 的正态分布; $\sum^{n}_{i=1}X_i$ 的分布近似于 $\mu_{\Sigma}=n\mu,\sigma^2_{\Sigma}=n\sigma^2$ 的正态分布
关于中心极限定理的证明,我们在后面的高级课程中给出,这里我们需要做到的是理解定理内容。
又一个🌰 :
从一个均匀分布中采样,假设从 $[0,1]$ 的均匀分布重采样得到 $n=12$ 个样本,求 $Pr(|\bar{X}_n-\frac{1}{2}|\leq 0.1)$ 的大概值。
解:
- $[0,1]$ 之间的均匀分布的期望是 $\frac{1}{2}$
- 方差是 $\sigma^2=\frac{1}{12}$
- 这里 $n=12$
- $\bar{X}_n$ 根据中心极限定理,其分布近似为 $\mu_{\bar{X}_n}=\frac{1}{2},\sigma_{\bar{X}_n}^2=\frac{1}{144}$
- 根据中心极限定理,设随机变量 $Z=12(\bar{X}_n-\frac{1}{2})$ 近似于标准正太分布,于是有:
$$
\begin{aligned}
Pr(|\bar{X}_n-\frac{1}{2}|\leq 0.1)&=Pr[12|\bar{X}_n-\frac{1}{2}|\leq 1.2]\\
&=Pr(|Z|\leq 1.2)\\
&\approx 2\Phi(1.2)-1\\
&=0.7698
\end{aligned}
$$
上面是书上的答案,但是我看有点问题就是第5步,根据中心极限定理 $Z=\frac{12^{1/2}(\bar{X}_n-\frac{1}{2})}{\frac{1}{12}}=24\sqrt{3}(\bar{X}_n-\frac{1}{2})$ 但不知道为啥直接被变成12了。
下面我们来介绍在中心极限定理里面出现的收敛在其他过程中的应用,以及他有自己的名字。
Definition Convergence in Distribution/Asymptotic Distribution.Let $X_1,X_2,\dots$ be a sequence of random variables,and for $n=1,2,\dots$ ,let $F_n$ denote the c.d.f. of $X_n$ .Also,let $F’$ be a c.d.f. Then it is said that the sequence $X_1,X_2,\dots$ converges in distribution to $F’$ if
$$
lim_{n\to \infty}F_n(x)=F’(x)
$$
for all x at which $F’(x)$ is continuous.Sometimes,it is simply said that $X_n$ converges in distribution to $F’$ ,and $F’$ is called the asymptotic distribution of X_n,If $F’$ has a name ,then we say that X_n converges in distribution to that name
定义收敛到分布,或者渐进分布:一个随机变量序列 $X_1,X_2,\dots$ 对应的c.d.f. 为$F_n$ 其中 $n=1,2\dots$ 并且 $F’$ 是一个c.d.f. 那么当 $lim_{n\to \infty}F_n(x)=F’(x)$ 时,我们说随机变量序列 $X_1,X_2,\dots$ 的分布收敛到 $F’$ 。 $x$ 对于所有 $F’(x)$ 都是连续的,有时候简单的说 $X_n$ 收敛到 $F’$ ,如果这个 $F’$ 有自己的名字,比如正态分布,我们就说 $X_n$ 收敛到正态分布。也可以说 $X_n$ 的渐进分布是正态分布。
根据上面的定义,我们可以说 $\frac{n^{1/2}(\bar{X}_n)-\mu}{\sigma}$ 收敛到标准正态分布。
中心极限定理也解释了为什么自然界中的大量数据都收敛到正态分布,比如人的身高,体重,收集足够的数据后会发现其收敛到正态分布。
Delta 方法 The Delta Method
🌰 :
服务时间问题,顾客们在排队,假设第 $i$ 个顾客到达柜台至完成服务用时 $X_i$ ,我们会得到 $X_1,X_2,\dots$ 共 $n$ 个随机变量,我们假设这些随机变量独立同分布,并且分布均值为 $\mu$ 方差为 $\sigma^2$ 那么我们可以根据中心极限定理给出 $\bar{X}_n$ 的分布,但是如果我们关心服务速度,也就是 $\frac{1}{\bar{X}_n}$ 那么我们改如何建模呢?
例子引出的问题,独立同分布随机变量样本期望可以用中心极限定理建模,如果这个期望经过某个函数变换呢?比如上面例子中的取倒数,如何对这个新的随机变量建模呢?
统计中一个已知的方法叫做 Delta方法,能够帮我们解决这个问题。
Theorem Delta Method. Let $Y_1,Y_2,\dots$ be a sequence of random variables,and let $F’$ be a continuous c.d.f. Let $\theta$ be a real number,and let $\alpha_1,\alpha_2,\dots$ be a sequence of positive numbers that increase to $\infty$ .Suppose that $a_n(Y_n-\theta)$ converges in distribution to $F’$ . Let $\alpha$ be a function with contimuous derivative such that $\alpha’(\theta)\neq 0$ .Then $a_n[\alpha(Y_n)-\alpha(\theta)]/\alpha’(\theta)$ converges in distribution to $F’$
一个随机变量序列的线性变换收敛到某分布,那么这个随机变量序列的某函数映射后的随机变量的线性变换依旧收敛到这个分布。
证明:
这个过程相对粗糙相当于给出了证明框架。
- $a_n\to\infty$ 的时候 $Y_n$ 会概率收敛到 $\theta$ 否则 $|a_n(Y_n-\theta)|\to \infty$ ,也就是不收敛。
- 因为 $\alpha$ 是连续函数, $\alpha(Y_n)$ 将会非常接近 $\alpha(\theta)$
- 使用泰勒级数(忽略更高阶项):
$$
\alpha(Y_n)\approx \alpha(\theta)+\alpha’(\theta)(Y_n-\theta)
$$ 两边同时减去 $\alpha(\theta)$ 后乘以 $\frac{a_n}{\alpha’(\theta)}$ 得到:
$$
\frac{a_n}{\alpha’(\theta)}(Y_n-\theta)\approx a_n(Y_n-\theta)
$$4中结论左右两边都收敛到 $F’$
这个定理给出的方法最常见的一个就是 $Y_n$ 是随机样本的平均数,随机样本的方差有限,可以得出以下推论。
Corollary Delta Method for Average of a Ramdom Sample.Let $X_1,X_2\dots$ be a sequence of i.i.d. random variables from a distribution with mean $\mu$ and finite variance $\sigma^2$ .Let $\alpha$ be a function with continuous derivative such that $\alpha’(\mu)\neq 0$ .Then the asymptotic distribution of
$$
\frac{n^{1/2}}{\sigma\alpha’(\mu)}[\alpha(\bar{X}_n)-\alpha(\mu)]
$$
is the standard normal distribution.
证明方法就是使用Delta法则,就能得到结果。
总结
本文介绍了中心极限定理的基础知识,因为本定理在概率论和数理统计中的超级低位,希望大家能仔细阅读文章内容。
下一篇我们对本章进行收尾,同时结束概率论基础部分。
