Abstract: 本文是关于Bayes’ Theorem 的介绍性知识
Keywords: Bayes’ Theorem,Law of total Probability
贝叶斯定理
今天的废话可能有点正经,就是关于Bayes’ Theorem的相关往事,做人脸识别的都会知道一个叫做联合Bayes的分类器,没错,我们当时做的时候也是第一个做了这个算法,当然,我没有自己去研究实践,最后结果不太理想,当然我不是说我去做结果就能好多少,其实投资也好做项目也好,失败向来不可怕,各种各样的死法在开始之前都有些预期,但是我们有一个期待,就是自己有个主观概率觉得我有90%可能会成功,前提是xx个项目能够顺利如期成功,但是当xx项目进展严重受阻,你就会重新评估成功概率,这个过程就可以用Bayes定理去建模;这个过程其实不可怕,最可怕的是你不知道你现在遇到了什么问题,你的小伙伴告诉你成功了,但其实根本没成功,有时候告诉你没成功,但是其实已经成功了,当一些事件结果变得不可信,那么你的评估将会变得毫无意义。
失败不可怕,可怕的是你不可控,说赚了三块钱,结果赔了五块,说赔了五块,结果赔了八块。
贝叶斯定理 Bayes’ Theorem
上面一个经典案例中包含了两个Bayes相关的经验,首先是一个具体的算法,用于分类,另一个是实现这个算法的过程产生的故事,也可以用贝叶斯公式来建模。
贝叶斯公式在概率论和统计中处于非常核心的部分,所以才有贝叶斯学派这种派系(不知道在我们社会主义伟大祖国,搞个这种学派是不是违法的)对立学派是频率派,这两派具体怎么样我们先不去深入区分,因为我们目前研究的境界还不需要站队,而就算有一天你需要站队了,这种站队可能出于利益和权利的考虑也要少很多,而是更多的源自自己觉得哪一派更接近真理。
- 频率学派的观点主要是认为所有事件的概率都不确定,但是可以用频率来近似得到。
- 贝叶斯派则认为所有事件的概率都是确定的,只是你的先验知识不足,所以算不出来而已。
大概可以这么理解,我们不再纠结上面这个关于上帝存不存在的问题,回到数学本身。
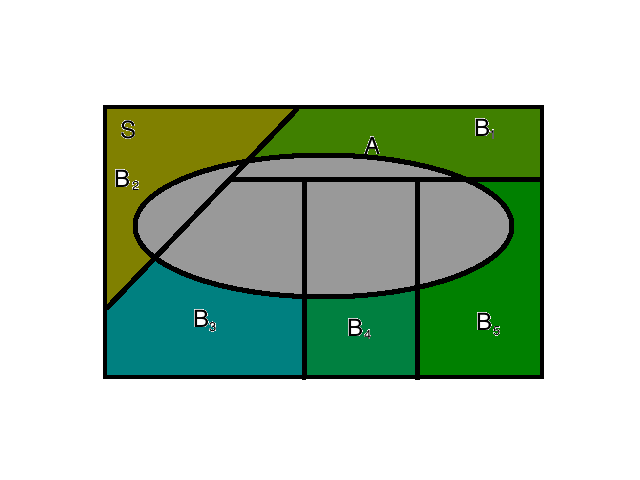
例如上图,来自全概率公式那一篇:当我们面对一个试验,在所有的partition中( $B_1\dots B_n$ )必然有一个将要发生,但不确定发生哪一个,我们可以观察到另一个事件A,如果已知$Pr(A|B_i)$ ,那么当我们确定A事件的发生概率的时候,就可以翻过来推到每个partition发生的概率有多大$Pr(B_i|A)$
上面这个是简单的逻辑分析,可以大概知道我们为啥要Bayes公式。
从分析上通过前面的条件概率公式可以非常轻松的得到贝叶斯公式:
$$
Pr(A\cap B)=Pr(A|B)Pr(B)=Pr(B|A)Pr(A)\\
Pr(A|B)=\frac{Pr(B|A)Pr(A)}{Pr(B)} \quad where \quad Pr(B)\neq 0\\
or\\
Pr(B|A)=\frac{Pr(A|B)Pr(B)}{Pr(A)} \quad where \quad Pr(A)\neq 0
$$
这个就是最简单的贝叶斯公式推到,同时可以用全概率公式进行代换,就能得到更专业的贝叶斯公式。
举个例子🌰 :
还是前面的随机拿螺丝,两个箱子A和B,我们随机选取一个箱子从里面拿螺丝(箱子有相等的概率被选中,所以 $Pr(A)=\frac{1}{2}$ ),已知A中有长螺丝6个短螺丝4个,B箱子有长螺丝3个短螺丝7个,设长螺丝为事件L短螺丝为事件S,那么可以有
$$
Pr(L|A)=\frac{6}{10}\\
Pr(S|A)=\frac{4}{10}\\
Pr(L|B)=\frac{3}{10}\\
Pr(S|B)=\frac{7}{10}\\
Pr(L)=Pr(L|A)Pr(A)+Pr(L|B)Pr(B)=\frac{6}{10}\times \frac{1}{2}+\frac{3}{10}\times \frac{1}{2}=0.45\\
Pr(S)=Pr(S|A)Pr(A)+Pr(S|B)Pr(B)=\frac{4}{10}\times \frac{1}{2}+\frac{7}{10}\times \frac{1}{2}=0.55
$$
现在我们已知拿出了一个长的螺丝,那么问从A箱子拿出来的概率是多少,从B箱子拿出来的概率是多少。
$$
Pr(A|L)=\frac{Pr(L|A)Pr(A)}{Pr(L)}=0.3/0.45=0.667\\
Pr(B|L)=\frac{Pr(L|B)Pr(B)}{Pr(L)}=0.15/0.45=0.333
$$
得出结论是A的可能性更高,因为A中长螺丝更多,这与我们的感觉上是一致的。
Theorem Bayes’ Theorem: Let the events $B_1\dots B_k$ from a partition of the space S such that $Pr(B_j)>0$ for $j=1,\dots ,k$ and let A be an event such that $Pr(A)>0$ , Then for $i=1,\dots,k$ :
$$
Pr(B_i|A)=\frac{Pr(B_i)Pr(A|B_i)}{Pr(A)}=\frac{Pr(B_i)Pr(A|B_i)}{\sum_{j=1}^{k}Pr(B_j)Pr(A|B_j)}
$$
这个就是普通的Bayes公式结合上全概率公式得出的一个比较实用的版本,证明这里就不详细写出来了,因为通过条件概率和全概率公式就能得出上面的结论,那么如此简单的一个公式为什么如此核心呢?
我们从哲理中分析一下,首先我们看 $Pr(B_i)$ 从本文第一张图片上可以看出来,这个划分从客观上说是是对完整样本空间的一个分别估计,这个过程与A是否发生无关,但当试验被观察到事件A发生了,我们的样本空间实际上发生了改变,不在是完整的S,因为$A^c$ 不可能发生了,这种情况下,我们将这个分割重新计算: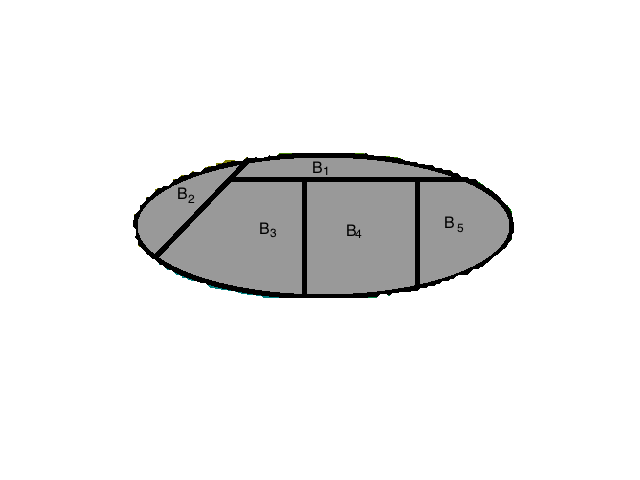
这个图是从上面的那幅图啃出来的,所以有点不整齐,这个整个过程就是贝叶斯要刻画的,样本空间的改变导致了整个划分的概率发生了不确定的变化,以前大的可能现在变得小到没有,现在大的可能之前非常小。
一般情况下,我们在实验开始之前已经知道了样本空间,以及它的“划分”,如果观察到某个划分发生了,我们可以相应的变更我们所关注的事件A,这是一般上的从原因推出结果,典型的概率论过程,已知原理推结果。
实际上我们不可能,也没能力知道这个划分,但是结果我们只要观察可能定能看到,于是我们通过结果A来反过来推这个划分是什么样子的,那么这个过程是个典型的数理统计过程,已知结果推原理,也叫贝叶斯统计。
条件贝叶斯定理 Conditional Version of Bayes’s Theorem
所有概率公式定理都可以改装成条件版本,Bayes’s Theorem也不例外,当然和原始公式基本一致:
$$
Pr(B_i|A\cap C)=\frac{Pr(B_i|C)Pr(A|B_i\cap C)}{\sum^k_{j=1}Pr(B_j|C)Pr(A|B_j\cap C)}
$$
对于扩展到条件概率,我们一般的做法就是给所有项的条件上都并上一个附加的事件。
先验概率,后验概率 Prior and Posterior Probabilities
我记得大学的时候学概率论的时候,第一次学贝叶斯公式,那时候老师跟我们说贝叶斯的每一项都有一个名字,先验,后验,似然值什么的,那时候没心思学习数学理论,考试的时候只能去背一下,结果一直也不知道啥意思,后来干活的时候,也遇到过Prior filter 和posterior filter,当时只知道一个前置滤波器,一个是后置滤波器,当看DeGroot的书的时候,看到Prior Probability和Posterior Probability才知道原来这个先验概率和后验概率是先于试验和后于试验的意思,很明显,等号前面的那个是要求的,肯定是试验后要计算的,肯定是后验概率,分母上的$Pr(B_i)$ 这个划分明显是试验之前知道的,故而叫做先验概率。
多步后验概率计算 Computation of Posterior Probabilities in More Than One Stage
这部分可以看做是个应用但是很有实际意义:
两个硬币,一个是正常的,A,两面不同 ${H,T}$ ,另一个是特制的B,两面相同都是 ${H}$ ,在我们不知道拿出了哪个硬币的前提下,丢硬币,第一次出现了$H_1$ 是个H,下标表示试验步数,那么我们可以使用贝叶斯计算:
$$
Pr(A|H_1)=\frac{Pr(H_1|A)Pr(A)}{Pr(H_1|A)Pr(A)+Pr(H_1|B)Pr(B)}=\frac{\frac{1}{2}\times \frac{1}{2}}{\frac{3}{4}}=\frac{1}{3}\\
Pr(B|H_1)=\frac{Pr(H_1|B)Pr(B)}{Pr(H_1|A)Pr(A)+Pr(H_1|B)Pr(B)}=\frac{1\times \frac{1}{2}}{\frac{3}{4}}=\frac{2}{3}
$$
这是第一步的结果,那么如果我们继续丢同一个硬币,观察结果,我们得到了$H_2$ 还是一个H,那么我们将得到条件版本的贝叶斯用法:
$$
Pr(A|H_1\cap H_2)\\
=\frac{Pr(H_2|A\cap H_1)Pr(A\cap H_1)}{Pr(H_2|A\cap H_1)Pr(A\cap H_1)+Pr(H_1|B\cap H_1)Pr(B\cap H_1)}\\
=\frac{Pr(H_2|A\cap H_1)Pr(A|H_1)Pr(H_1)}{Pr(H_2|A\cap H_1)Pr(A|H_1)Pr(H_1)+Pr(H_1|B\cap H_1)Pr(B| H_1)Pr(H_1)}\\
=\frac{Pr(H_2|A\cap H_1)Pr(A|H_1)}{Pr(H_2|A\cap H_1)Pr(A|H_1)+Pr(H_1|B\cap H_1)Pr(B| H_1)}
$$
上述过程对于B是一样的,通过条件概率的公式,可以化简得到上述公式,通过对比,我们发现两步的差别就是第二步的Prior 是第一步的posterior,如果是多步的试验,可以完全满足这个规律上一步的posterior用作下一步的prior
这种和我们现实中的各种推理完全符合,我们通过推理分析,修改了我们最初的估计,并实现在估计更接近事实,这就是个进化过程。
计算得出我们第二步的结果:
$$
Pr(A|H_1\cap H_2)=\frac{1}{5}\\
Pr(B|H_1\cap H_2)=\frac{4}{5}
$$
这是符合我们的感觉的,出现H越多,A的可能性就越低。
条件独立事件 Conditionally Independent Events
概要观察上面这个丢硬币的例子,$H_2$ 的出现和 $H_1$ 的出现应该是相互独立的,但是结合上面的计算我们发现当$H_1$ 发生的时候,$H_2$的不确定性被影响了,所以在A和B不确定时,并不独立,但是当我们确定是一个正常的硬币,也就是A确定发生的时候,$H_1$ 和 $H_2$ 独立。
而且我们观察上面的计算过程,如果我们继续算下去,当前步骤的先验概率(上一步中的后验概率)会逐渐收敛,而不论初始值是什么:1
2
3
4
5
6
7
8
9
10
11
12N = 10
P_a_=0.5
P_b_=0.5
for i in range(N):
P_a_hi_=(P_a_*0.5)/(P_a_*0.5+P_b_*1.0)
P_b_hi_=(P_b_*1)/(P_a_*0.5+P_b_*1.0)
P_a_=P_a_hi_
P_b_=P_b_hi_
print "$Pr(A|\\bigcap^"+ `i` + " H_i" + ")=" + "%0.6f" %P_a_ + \
";Pr(B|\\bigcap^"+ `i` + " H_i" + ")=" + "%0.6f" %P_b_ +"$"
跑了下结果:
当$Pr(A)=0.1$ 和 $Pr(B)=0.9$ 时:
$Pr(A|\bigcap^0 H_i)=0.052632;Pr(B|\bigcap^0 H_i)=0.947368$
$Pr(A|\bigcap^1 H_i)=0.027027;Pr(B|\bigcap^1 H_i)=0.972973$
$Pr(A|\bigcap^2 H_i)=0.013699;Pr(B|\bigcap^2 H_i)=0.986301$
$Pr(A|\bigcap^3 H_i)=0.006897;Pr(B|\bigcap^3 H_i)=0.993103$
$Pr(A|\bigcap^4 H_i)=0.003460;Pr(B|\bigcap^4 H_i)=0.996540$
$Pr(A|\bigcap^5 H_i)=0.001733;Pr(B|\bigcap^5 H_i)=0.998267$
$Pr(A|\bigcap^6 H_i)=0.000867;Pr(B|\bigcap^6 H_i)=0.999133$
$Pr(A|\bigcap^7 H_i)=0.000434;Pr(B|\bigcap^7 H_i)=0.999566$
$Pr(A|\bigcap^8 H_i)=0.000217;Pr(B|\bigcap^8 H_i)=0.999783$
$Pr(A|\bigcap^9 H_i)=0.000108;Pr(B|\bigcap^9 H_i)=0.999892$
当$Pr(A)=0.5$ 和 $Pr(B)=0.5$ 时:
$Pr(A|\bigcap^0 H_i)=0.333333;Pr(B|\bigcap^0 H_i)=0.666667$
$Pr(A|\bigcap^1 H_i)=0.200000;Pr(B|\bigcap^1 H_i)=0.800000$
$Pr(A|\bigcap^2 H_i)=0.111111;Pr(B|\bigcap^2 H_i)=0.888889$
$Pr(A|\bigcap^3 H_i)=0.058824;Pr(B|\bigcap^3 H_i)=0.941176$
$Pr(A|\bigcap^4 H_i)=0.030303;Pr(B|\bigcap^4 H_i)=0.969697$
$Pr(A|\bigcap^5 H_i)=0.015385;Pr(B|\bigcap^5 H_i)=0.984615$
$Pr(A|\bigcap^6 H_i)=0.007752;Pr(B|\bigcap^6 H_i)=0.992248$
$Pr(A|\bigcap^7 H_i)=0.003891;Pr(B|\bigcap^7 H_i)=0.996109$
$Pr(A|\bigcap^8 H_i)=0.001949;Pr(B|\bigcap^8 H_i)=0.998051$
$Pr(A|\bigcap^9 H_i)=0.000976;Pr(B|\bigcap^9 H_i)=0.999024$
当$Pr(A)=0.9$ 和 $Pr(B)=0.1$ 时:
$Pr(A|\bigcap^0 H_i)=0.818182;Pr(B|\bigcap^0 H_i)=0.181818$
$Pr(A|\bigcap^1 H_i)=0.692308;Pr(B|\bigcap^1 H_i)=0.307692$
$Pr(A|\bigcap^2 H_i)=0.529412;Pr(B|\bigcap^2 H_i)=0.470588$
$Pr(A|\bigcap^3 H_i)=0.360000;Pr(B|\bigcap^3 H_i)=0.640000$
$Pr(A|\bigcap^4 H_i)=0.219512;Pr(B|\bigcap^4 H_i)=0.780488$
$Pr(A|\bigcap^5 H_i)=0.123288;Pr(B|\bigcap^5 H_i)=0.876712$
$Pr(A|\bigcap^6 H_i)=0.065693;Pr(B|\bigcap^6 H_i)=0.934307$
$Pr(A|\bigcap^7 H_i)=0.033962;Pr(B|\bigcap^7 H_i)=0.966038$
$Pr(A|\bigcap^8 H_i)=0.017274;Pr(B|\bigcap^8 H_i)=0.982726$
$Pr(A|\bigcap^9 H_i)=0.008712;Pr(B|\bigcap^9 H_i)=0.991288$
当次数足够多的时候,会收敛到一个常数值,为什么呢?我们可以去研究一下他的递推公式
$$
x_i=\frac{ax_{i-1}}{ax_{i-1}+b(1-x_{i-1})}
$$
没算出来具体怎么收敛,数分还没学好,如果后面会了回来算一下。
补充个例子:
某种病毒在人口中的携带率是$Pr(pv)=0.03$ (pv,nv分别代表携带病毒和不携带病毒)检测的时候中会出现一下情况(有机器学习经验同学会对这个非常熟悉,包括True Positive (TP),False Positive (FP),False Negtive (FN),True Negtive (TP)):
$$
Pr(P|pv)=0.99\\
Pr(P|nv)=0.05\\
Pr(N|pv)=0.01\\
Pr(N|nv)=0.95\\
$$
当假定某人被检测其携带病毒,那么此人携带病毒的概率是多大?
- 我们没文化,根据实验说明,我们有99% 的概率携带病毒,如果病毒致死律很高,这个概率足以让你准备后事。
- 如果我们有文化,考虑下先验知识,病毒本身携带率那么低,当我们被检出携带病毒,那么我们结合携带率和实验准确度,可以得出:$Pr(pv|P)=\frac{Pr(P|pv)Pr(pv)}{Pr(P|pv)Pr(pv)+Pr(P|nv)Pr(nv)}=\frac{0.03\times 0.99}{0.03\times 0.99+0.97\times 0.05}=0.380$ ,这个看起来还可以抢救一下
这种实验的关键是提高准确率也就是0.99需要更高比如0.9999999,这是后检测结果更接近真实结果,0.99会产生大量虚报,这个在机器学习上非常有用!
总结
引用陈希孺先生的一句话总结:“概率思维是人们正确观察事物必备的文化修养,这样说并不过分”。
有文化真好。
