Abstract: 本文介绍事件的独立，以及派生出来的多事件独立，以及条件独立
Keywords: Independent Events，Independent of Several Events，Coditionally Independent Events

独立事件

今天想说的废话就是，其实什么行业想做的好都要靠知识，做软件是这样，硬件也是，说相声是，其他行业也是，刚开始可能觉得经验丰富的人可以很顺利的做好任何我们觉得很难的事，过了三五年发现我们自己也可以很顺利的完成了，我们就变得优秀了么？其实不是，时间成本决定了你可以在不太努力的情况下成长，但是这种成长速度不足以让你成为行业顶级人物，当然不是所有人都想做顶级，想做顶级，必须强迫自己去做一些舒适区以外的事情。
从根本上思考理解自己做的事，同时有计划的训练才是野蛮生长的最快途径。
美国人Noel Tichy提出的理论，图里的3个区可以表示为你想学习的事物的等级:

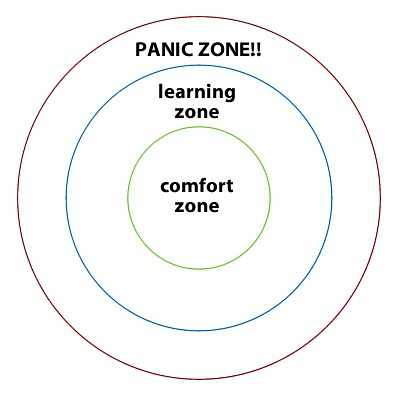
不要停留在舒适区，也不要好高骛远的直接去Panic Zone，那样会死的很惨，多去学习区，这样才能不断的进步。

独立事件 Independent Events

上一篇我们讲到条件概率，这一篇其实是和上一篇同样的研究两个事件间的关系的，条件概率最朴素的想法就是当一个事件发生了，其对我们关心的事件是否发生有没有影响，有影响与否这都是个条件概率，如果没有影响，我们进一步把这两个事件称之为独立的。
独立与互斥，对立等意义都不相同，独立性是概率论的重要基础关系，在独立事件上建立的概率论理论已经很完备了，但是对于非独立事件相关的研究开在继续完善中，很多情况下我们都是假设，或者近似一些事件独立的，来是模型更加简单准确。
我们上一篇中说的条件概率，假定我们已知事件B发生，那么事件A发生的概率在此条件下发生的概率是$Pr(A|B)$ 如果我们进一步说，B事件的发生与否对于A事件来说没有什么影响，那么我们就有$Pr(A|B)=Pr(A)$
上文中我们有一个很重要的乘法定义（条件概率定义引出的）
$$
Pr(A|B)=\frac{Pr(A\cap B)}{Pr(B)}\quad where \quad Pr(B)>0\\
Pr(A\cap B)=Pr(A|B)Pr(B) \quad where \quad Pr(B)>0
$$
那么当我们带入$Pr(A|B)=Pr(A)$ 可以得到一个让我们一直使用到去世的关系：
$$
Pr(A\cap B)=Pr(A)Pr(B)
$$
以上关系成立的充分必要条件是，事件A和事件B相互独立。

两个事件独立 Independence of Two Events

Definition Independent Events.Two events A and B are independent if
$$
Pr(A\cap B)=Pr(A)Pr(B)
$$

定义是说如果事件A和事件B满足上述关系，那么他们独立，注意，对于数学定义来讲，其条件会完全在定义的条件中体现，如果没有，那么就说明没限制。

举个🌰 ：
两个机器甲和乙，之间没有影响，独立工作，事件A表示甲工作三小时后坏掉$Pr(A)=\frac{1}{4}$，事件B表示乙工作山小时后坏掉$Pr(B)=\frac{1}{3}$，那么，当甲乙同时开始工作三个小时，那么他俩一起坏掉的概率是多少？

分析：甲乙之间独立，互不影响，所以从原理上满足组成复合事件时互相独立，那么$Pr(A\cap B)=Pr(A)Pr(B)=\frac{1}{4}\times \frac{1}{3}=\frac{1}{12}$

互斥事件和独立事件 Exclusive Events and independent Events

说一个我之前初学概率时的一个思维误区:
我一直以为独立在集合上的反映就是不想交，，像这样：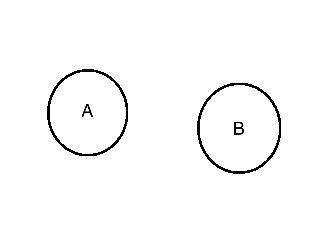

这是一种很自然的想法，当题设的条件中用到独立，互不影响地进进行两个实验的时候，我们很自然的把他们理解为两个样本空间，所以打死不会有交集，但事实是我们关心的是这两个试验的一个复合结果产生的样本空间。

但事实是这是个明显错误的，当A和B事件作为同一个试验的事件，那么当B发生的时候严重影响A的概率，因为当B发生的时候，A不可能发生，根据1-1中的T1，我们可以确定当$Pr(B)\geq 0$ 的时候 $Pr(A|B)=\frac{Pr(A\cap B)}{Pr(B)}=\frac{Pr(\emptyset)}{Pr(B)}=0$
这是个对立事件，不是独立事件。

分析独立事件的定义，我们可以看出独立并不等于不想交，从频率角度的解释是相交部分的面积占事件B的比例，刚好等于事件A面积对整个样本空间的面积比例:

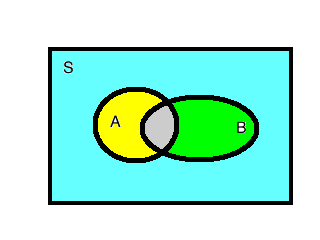
用图像的理解，A的面积与整体S的面积比等于灰色与B面积的比。

更深入的说，试验甲可能会产生一个包含10个事件 $A_1\dots A_{10}$ 的样本空间，试验乙可能会产生一个包含5个事件 $B_1\dots A_5$ 的样本空间，于是我们组合出来$10\times 5=50$ 个复合事件的样本空间（笛卡尔积，或者使用事件的乘法原理），我们关心的是这50个复合事件中的某个事件的概率；这时才是考虑组成复合事件的基本事件独立与否的时候，而不应该是脱离了复合事件直接分开考虑$A_i$ 和 $B_i$ 之间的独立性。
前一篇说过图像只能帮我们初步的感受其大概的意思，分析学方法才能帮助我们从逻辑的角度深入研究，分析方法就是看定义的公式，如果$Pr(A)\neq 0$ 和 $Pr(B)\neq 0$ ，那么交集的概率必然不是0，所以A与B必然有交集。

补集之间的独立 Independence of Complements

如果我们说两个事件独立了，其相交的事件的概率和这两个事件的关系会被确定，同样我们能得到其补集间的关系：

Theorem If two events A and B are independent,then the events $A$ and $B^c$ are also independent.

怎么证明呢，书上写的比较跳跃，我来补充下：
$$
A=(A\cap B^c)\cup(A\cap B)\\
Pr(A)=Pr(A\cap B^c)+Pr(A\cap B)\\
Pr(A\cap B)=Pr(A)Pr(B)\\
Pr(A\cap B^c)=Pr(A)-Pr(A)Pr(B)=Pr(A)(1-Pr(B))=Pr(A)Pr(B^c)
$$
Q.E.D
上面第一步是集合论知识，第二步是[1-1]中的T2，接着第四步是[1-1]中的T3，证毕。

根据上面的结论，当事件$A$ 和$B$ 独立的时候，那么$A$ 和$B^c$ 独立，继续推导$A^c$ 和$B^c$ 独立。

多事件独立 Independent of Several Events

把两个事件扩展到多个事件稍微有点复杂，从原理上讲，这些独立的事件里，某一个或者某几个发生并不影响其他事件发生的概率，那么他们就是独立的

Definition Mutually Independent Events The k events $A_1,\dots,A_k$ are independent or mutually independent if for every subset $A_{i_1},\dots,A_{i_j}$ of j of these events($j=2,3,\dots,k$)
$$
Pr(A_{i_1}\cap \dots \cap A_{i_j} )=Pr(A_{i_1})\dots Pr(A_{i_j})
$$

这个定义其实看起来有点费力，尤其是当出现两重下标的时候，公式显得复杂很多，但是如果看过分析类的书就可以用一种很简单的方式解释，那就是对于下标 $i_j$ 我们可以把它看成一个 $i(j):N\to N$的映射，映射从 $[1,k]$ 映射到 $[1,k]$ 可以出现多对一，这样就会产生一个子集，而上面的表示可以产生一个集合的全部子集，可以用排列的方式计算一共有多少。

用中文表示一下就是一组事件独立，当其全部子集内的事件都是独立的，那么这组事件相互独立，还是个递归定义，三个事件的组合要通过两个事件的独立验证，四个事件独立要用三个事件和两个事件的独立来验证。

例如：

当
$$
Pr(A\cap B)=Pr(A)Pr(B)\\
Pr(A\cap C)=Pr(A)Pr(C)\\
Pr(B\cap C)=Pr(B)Pr(C)\\
Pr(A\cap B\cap C)=Pr(A)Pr(B)Pr(C)
$$
必须满足上述四个关系，才能能保证三个事件独立。

但是

$Pr(A\cap B\cap C)=Pr(A)Pr(B)Pr(C)$ 不能保证三个事件独立
这三个也不行
$$
Pr(A\cap B)=Pr(A)Pr(B)\\
Pr(A\cap C)=Pr(A)Pr(C)\\
Pr(B\cap C)=Pr(B)Pr(C)\\
$$

下面的这个例子，说明这个情况：
在扔两个硬币的样本空间$S={HH,HT,TH,TT}$下有以下几个事件：

①$A={HH,HT}$

②$B={HH,TH}$

③$C={HH,TT}$

那么$A\cap B \cap C=A\cap B=B\cap C=A\cap C={HH}$
$$
Pr(A\cap B)=Pr(B\cap C)=Pr(A\cap C)=Pr(A\cap B \cap C)=\frac{1}{4}
$$
同时满足
$$
Pr(A\cap B)=Pr(A)Pr(B)\\
Pr(A\cap C)=Pr(A)Pr(C)\\
Pr(B\cap C)=Pr(B)Pr(C)\\
$$
但是不满足$Pr(A\cap B\cap C)=Pr(A)Pr(B)Pr(C)$ 所以三个事件相互不独立。

上面例子也好定理也好，都是要强调完整的子集和的集合。

独立和条件概率 Independence and Conditional Probability

补充个多事件独立的条件概率的定义：

Theorem Let $A_1,A_2,\dots,A_k$ be events such that $Pr(A_1\cap \dots \cap A_k)>0$ .Then $A_1\dots A_m$ and $A_1\dots A_l$ of$A_1\dots A_k$ we have
$$
Pr(A_{i_1}\cap \dots \cap A_{i_m}|A_{j_1}\cap \dots \cap A_{j_l})=Pr(A_{i_1}\cap \dots \cap A_{i_m})
$$
这个解释是两个事件的独立的条件理解的扩展，这里不再过多解释啦。

条件独立事件 Coditionally Independent Events

条件概率上一篇就说到了，我们可以给任何事件的概率加上条件，只是有些可以不加，或者省略，而且条件概率的所有性质，定理，公理都与概率一致（因为所有概率都是条件的）。那我们就顺着这个思路，个独立事件加上条件，称之为条件独立。条件独立更加复杂，当然也更加通用。但其定义方法及其简单，我们直接对多个事件的定义下手，两个事件的条件独立被包含在其中：

Theorem Conditional Independence We say that event $A_1\dots A_k$ are conditional independent given B if,for every subcollection $A_{i_1},\dots ,A_{i_j}$ of $j$ of these events ($j=2,3,\dots,k$)
$$
Pr(A_{i_1}\cap \dots \cap A_{i_j}|B)=Pr(A_{i_1}|B)\dots Pr(A_{i_j}|B)
$$

这个定义的解释和上面多事件的解释基本一致，一组事件在条件B下独立的条件是他的所有子集的组合都是在条件B下独立的。

对于两个事件的条件独立，我们有下面这个定理

Theorem Suppose that $A_1,A_2$ and $B$ are events such that $Pr(A_1\cap B)>0$ Then $A_1$ and $A_2$ are conditional independent given $B$ if and only if $Pr(A_2|A_1\cap B)=Pr(A_2|B)$

总结

总结就一句话，掌握了这一句就掌握了这一篇的所有，什么是独立，互不影响就是独立

人工智能基础

【概率论】2-2:独立事件(Independent Events)