Abstract: 本文主要介绍行列式的应用,包括求逆,求面积,求体积,以及叉乘的一些性质
Keywords: Inverses,Cramer’s Rule,Volumes,Determinant,Cross Product
克莱姆法则,逆和体积
废话已经变成每篇的例行公事了,不过我们还是来嘲笑一下Apple这个“垃圾”公司,憋了三五年搞出来个iPhone x,连个双胞胎都识别不出来,我们国内的各大小厂商随便搞个平面摄像头就搞定的简单任务,apple这么大个公司,用了三维图像都搞不出来,被各大网友嘲笑,其实之前好多VC都问我:“你这个识别双胞胎行不行”,我说,“No”,然后大哥语重心长的对我说“别人xx都能识别,你这个技术不到位啊”,以上对话真实存在,而且发生了好多次,后来我们的宣传口号就是”我们的摄像头亩产1亿斤小麦”,哈哈哈。希望业界技术能不断推陈出新,不断再创新高,也祝给为VC投资都有回报,祝那些双胞胎人脸准确率继续攀升。
克莱姆法则
Cramer应该是行列式研究比较关键的一个人,但绝对不是第一个人,他应该是把行列式单独出来研究的数学家,但是最一开始用行列式解方程的可能是莱布尼兹,所以行列式发明伊始毫无疑问是用来解方程的。Cramer法则也是用来解方程的,顺便也能求个逆什么的。
$Ax=b$
$Ax=b$ 我们已经研究了有一段时间了,但是我们今天还要继续通过研究旧的知识来得到新的知识,其实数学知识体系应该就是这样的,一开始有几个公理,然后逐渐通过推导,证明, 定义,引申,出来一个完整的数学体系,读陶哲轩的《analysis》和陈希孺的《概率与数理统计》都给人一种这个感觉,很简单的几个公理,能推导出一些列非常惊艳的理论和体系,然后经过我们专家们的努力,变成了各种难度的考试题。
Key Idea:
$$
\begin{bmatrix}
&&\\&A&\\&&
\end{bmatrix}
\begin{bmatrix}
x_1&0&0\\x_2&1&0\\x_3&0&1
\end{bmatrix}=
\begin{bmatrix}
b_1&a_{12}&a_{13}\\b_2&a_{22}&a_{23}\\b_3&a_{32}&a_{33}
\end{bmatrix}=B_1
$$
这个大家应该都理解了,如果按照列空间的模式来看,就是 $\vec{B}$ 被A矩阵射到列空间,然后为了和谐将 $\begin{bmatrix}0\\1\\0\end{bmatrix}$ 和 $\begin{bmatrix}0\\0\\1\end{bmatrix}$ 陪射到列空间,然后拼起来就是个矩阵乘矩阵等于矩阵了,这样有个非常不错的效果就是 $\begin{bmatrix}x_1&0&0\\x_2&1&0\\x_3&0&1\end{bmatrix}$ 这货的行列式是 $x_1$ ,那就可以了,利用行列式的性质,两边去行列式就有了
$$
det(A)det(\begin{bmatrix}x_1&0&0\\x_2&1&0\\x_3&0&1\end{bmatrix})
=det(A)x_1\\
=det(\begin{bmatrix}b_1&a_{12}&a_{13}\\b_2&a_{22}&a_{23}\\b_3&a_{32}&a_{33}\end{bmatrix})
=det(B_1)\\
x_1=\frac{det(B_1)}{det(A)}
$$
这样就有了 $x_1$ ; $x_2$ 类似:
$$
det(A)det(\begin{bmatrix}1&x_1&0\\0&x_2&0\\0&x_3&1\end{bmatrix})
=det(A)x_2\\
=det(\begin{bmatrix}a_{11}&b_1&a_{13}\\a_{21}&b_2&a_{23}\\a_{31}&b_3&a_{33}\end{bmatrix})
=det(B_2)\\
x_2=\frac{det(B_2)}{det(A)}
$$
按照这个方式可以完整的求出 $\vec{x}$ ,这个就Cramer’s Rule的思想描述,前提是det(A)不等于0,完整描述:
$$
x_1=\frac{det(B_1)}{det(A)}\\
x_2=\frac{det(B_2)}{det(A)}\\
\vdots\\
x_n=\frac{det(B_n)}{det(A)}
$$
观察下计算量: $O(det(A))=n!$ , $O(det(B_i))=n!$ (i=1,2…n) 所以总计算量 $(n+1)!$ 如果n=10,计算量过百万次,并且飞速增长,于是得出结论,别管是计算机还是人,这个法则适合矩阵小的时候,大了不适合。
$AA^{-1}=I$
从上面的解方程可以很自然的引申到求逆,稍加改装就行了:
$$
\begin{bmatrix}
&&\\&A&\\&&
\end{bmatrix}
\begin{bmatrix}
x_{11}&x_{12}&x_{13}\\
x_{21}&x_{22}&x_{23}\\
x_{31}&x_{32}&x_{33}
\end{bmatrix}=
\begin{bmatrix}
1&0&0\\0&1&0\\0&0&1
\end{bmatrix}
$$
这个改装的不明显?那好我再把它打碎一些:
$$
\begin{bmatrix}
&&\\&A&\\&&
\end{bmatrix}
\begin{bmatrix}
x_{11}&0&0\\
x_{21}&1&0\\
x_{31}&0&1
\end{bmatrix}=
\begin{bmatrix}
1&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&a_{32}&a_{33}
\end{bmatrix}=B_1
$$
怎么样,这样清晰了吧,我们还是用Cramer法则,得到的 $x_{11}=\frac{det(I_1)}{det(A)}$ 这个就是Cramer法则的公式的带入,如果没看懂,请回到上一小节,接着我们分析下矩阵 $\begin{bmatrix}1&a_{12}&a_{13}\\0&a_{22}&a_{23}\\0&a_{32}&a_{33}\end{bmatrix}=I_1$ 这个矩阵厉害的地方在于他的行列式等于第一个元素1的cofactor,即 $det(B_1)=C_{11}=\begin{vmatrix}a_{22}&a_{23}\\a_{32}&a_{33}\end{vmatrix}$,厉害不厉害,那么 $x_{11}=\frac{det(B_1)}{det(A)}$ 也就是 $x_{11}=\frac{C_{11}}{det(A)}$ 同理可以推出 $x_{21}=\frac{C_{12}}{det(A)}$ ,$x_{31}=\frac{C_{13}}{det(A)}$
那么这么继续下去(这里跳过了基本步骤,不明白可以回到Cramer 法则,一毛一样的过程),得到了$A^{-1}$ :
$$
A^{-1}_{ij}=\frac{C_{ji}}{det(A)}
$$
这个就是矩阵求逆的公式,我记得我当时学的时候这个公式老师写在黑板上,然后就让我们套着这个公式做算数练习了(MDZZ)。。
上面的公式可以反过来证明一下:
$$
\begin{bmatrix}
a_{11}&a_{12}&a_{13}\\
a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}
\end{bmatrix}
\begin{bmatrix}
C_{11}&C_{12}&C_{13}\\
C_{21}&C_{22}&C_{23}\\
C_{31}&C_{32}&C_{33}
\end{bmatrix}=
\begin{bmatrix}
det(A)&0&0\\
0&det(A)&0\\
0&0&det(A)
\end{bmatrix}
$$
这里等于det(A)的点我们就不算了,因为是公式,我们只算为0的点,比如 $\begin{bmatrix}a_{21}&a_{22}&a_{23}\end{bmatrix}$ 这个行向量,和 $\begin{bmatrix}C_{11}\\C_{21}\\C_{31}\end{bmatrix}$ 相乘 $a_{21}C{11}+a_{22}C_{12}+a_{23}C_{13}$ ,因为C也是从矩阵A构建出来的,我们给他来个大还原
$$
\begin{bmatrix}
a_{21}&a_{22}&a_{23}\\
a_{21}&a_{22}&a_{23}\\
a_{31}&a_{32}&a_{33}
\end{bmatrix}
$$
这个矩阵的行列式就是 $a_{21}C{11}+a_{22}C_{12}+a_{23}C_{13}$ 很明显更两行相等,就是说行列式值为0
一个不错的例题,如果cofactors都不是0,那么行列式一定非零么?答案当然是否定的,因为行列式最后是对cofactor加权求和的。
三角形面积
三角行的面积底乘以高除以2,小学版本的面积,升级以后的就是类似于用正弦函数在已知一个角和这个角的两条边的情况下,$S=ab \cdot sin(\theta)$ 这个应该算是比较高级的,但是我们分析下这两种常用的公式,里面需要用到的信息是什么?底乘以高,这里明显有两个长度,但是高隐藏了一个角度就是90度这个角至关重要,第二个ab是两条边的长度,和一个角度;也就是说求三角形面积,两个长度和一个角度是必不可少的,或者你也可以知道三个长度,根据余弦定理可以求出角。
回顾下向量,向量有方向,有长度,那么两个向量是不是就能求出三角行的面积?答案是肯定的,用前面的知识也很好求出,但是下面我们将学会一种很有趣的求法,没错,用行列式求面积:
如果一个三角形的三个顶点是 $(x_1,y_1)$ , $(x_2,y_2)$ , $(x_3,y_3)$ 那么三角形的面积是:
$$
Area=\begin{vmatrix}
x_1&y_1&1\\x_2&y_2&1\\x_3&y_3&1
\end{vmatrix}
$$
你可以把它记做公式或者怎么样,但是我觉得没必要,具体的证明?我不想写了,因为证明就是计算行列式,最后结果与其他方法算出来的相同,然后证毕。
下面的证明是非常有趣的一种方法,没有计算,而是巧妙的利用行列式的性质。
我们定义行列式的时候并不是上来就给力计算公式,而是规定了三个性质,通过这三个基本性质逐步形成了行列式的其他性质以及计算公式,再推广到应用,那么我们可以继续这种方法来把三角形的面积推广到平行四边形,对于平行四边形面积的性质:
- A=I 的平行四边形,面积是1
- 交换任意两行,面积不变(绝对值),行列式绝对值不变,只是要变号
- 满足加法和乘法原理,如果一条边乘以2(也就是行列式中的一行),那么面积要乘以2 ,与行列式性质相同,如果变增长一部分相当于延长,在行列式上的直接反应也是增加了一个行列式(另一块的面积),具体如下图
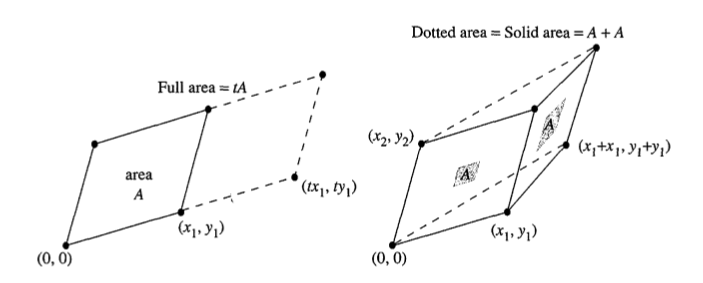
如果不明白A是什么,A是像三角形那个行列式一样,各顶点组合出来的。
这样的话就能证明行列式就是面积,具体是谁的面积,就是以各行为坐标,圈起来的图形的面积。
比如2x2的矩阵就是平行四边形的以原点为一个顶点,另外两个点是矩阵的行,推广到体积同样成立,
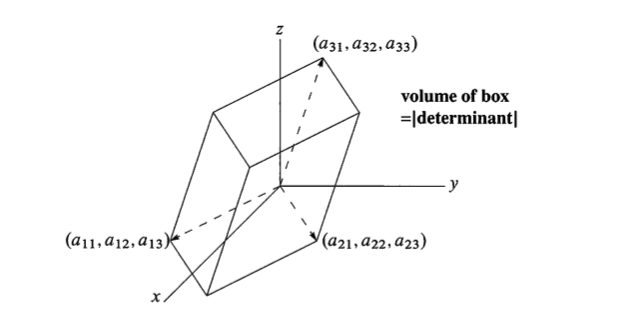
这里就不再继续描述了,因为大道理就上面的三条性质。
下面我们要正式回应一下本章开头提出的懵逼场景2(点击查看),也就是二重积分转换成极坐标的那个带入问题,其实问题的根源在于对于$dA=dxdy$ 是一种简单的形式,或者叫做一个结果,他求的是矩形面积,忽略了其中角度的关系,原始的$dA$ 应该是一个行列式比如对于直角坐标系,对x和y求二重微分
$dx=1dx+0dy$ 以及 $dx=0dx+1dy$ 那么写成矩阵形式就是下面的样子
$$
dA=
det(\begin{bmatrix}dx&0\\0&dy\end{bmatrix}
\begin{bmatrix}
1&0\\0&1
\end{bmatrix})
$$
也就是说我们要把坐标系的基矩阵也跟在后面,而前面是变量之间的微分关系(这个微分关系叫做雅克比矩阵)这个矩阵最后算出来的是一个伸缩比例,什么的伸缩比例?因为你已经把积分的单元改变了,之前那个dA和现在的dA不是一个同一个大小了,而是多了一个比例系数,以及两种不同积分元。
如果我们对积分变量进行代换,原变量为 $\vec{x}=x_1,x_2,\dots ,x_n$ 换元后的变量是 $\vec{y}=y_1,y_2,\dots ,y_n$ 并且满足 $x=Ay$ 那么 $d\vec{x}=J(A)d\vec{y}$
雅克比矩阵J(A):
$$
J=\begin{bmatrix}
\frac{\partial x_1}{y_1}&\dots&\frac{\partial x_1}{y_n}\\
\frac{\partial x_2}{y_1}&\dots&\frac{\partial x_2}{y_n}\\
&\vdots&\\
\frac{\partial x_n}{y_1}&\dots&\frac{\partial x_n}{y_n}
\end{bmatrix}
$$
然后根据行列式性质,两边同时行列式,就得到了新的积分元了,雅克比行列式提供了一个伸缩比例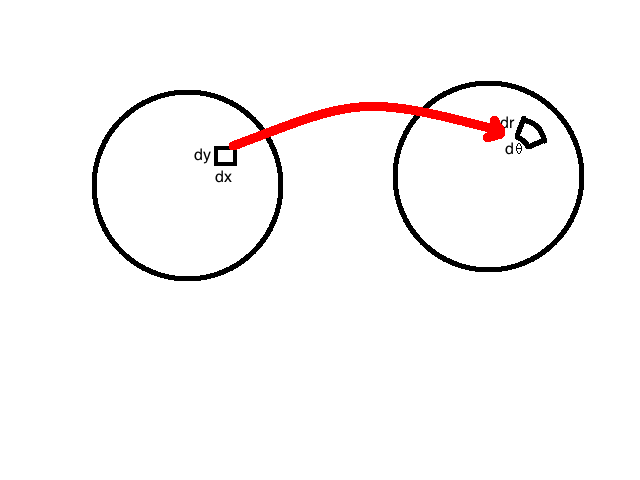
积分元的大小明显发生了变换,伸缩比例就是雅克比行列式的值。
叉乘
Cross Product与dot Product相对应,其结果是个新的向量而不是一个值,Cross的定义:
$$
u \times v =
\begin{vmatrix}
i&j&k\\
u_1&u_2&u_3\\
v_1&v_2&v_3
\end{vmatrix}
$$
得到的矩阵和u和v都正交,证明?
直接乘进去就有了
$$
\begin{vmatrix}
i&j&k\\
u_1&u_2&u_3\\
v_1&v_2&v_3
\end{vmatrix}
=i C_{11}-j C_{12}+k C_{13}
$$
那么进行dot product就有:
$$
\langle C_{11},-C_{12},C_{13}\rangle \cdot \langle u_1,u_2,u_3\rangle =
\begin{vmatrix}
u_1&u_2&u_3\\
u_1&u_2&u_3\\
v_1&v_2&v_3
\end{vmatrix}=0
$$
同理可以得到v,所以两个向量的cross product与这两个向量组成的平面垂直,方向满足右手定则(这个google下自己比划)
那么总结下Cross的性质
- $u \times v=- v \times u$
- $u \cdot (u \times v)=0$ and so do $v \cdot (u \times v)=0$
- $u \times u=0$ 自杀式cross行为,自己cross自己,等于灰飞烟灭
根据上一节和这一节的对比,连个向量的cross等于这两个向量为边的平行四边形面积,也就是说
$$
|u \times v| =|u||v|sin(\theta)
$$
方向满足右手定则。
Triple Product = Determinant = Volumes
推广到三维
$$
(u \times v)\cdot w=
\begin{vmatrix}
w_1&w_2&w_3\\
u_1&u_2&u_3\\
v_1&v_2&v_3
\end{vmatrix}=volume
$$
这个就是前面的简单推广,大家可以自己研究一下
总结
这篇没想到这么长,从早上写到下午,有问题请大家指出。。明天继续。。
