Abstract: 用大学的方法消元，也就是整个消元过程矩阵化，引出矩阵乘法
Keywords: Elimination Matrix，Matrix Multiplication，Augmented Matrix

本课视频课程已上线：使用矩阵消元

消元与矩阵的关系

发现这个教材真的很有章法，从big picture 的角度来看，所有知识环环相扣，每一环单独看还都不难，组合起来发现整个知识体系就完整了，我至今不懂为啥我们伟大社会主义中国的学者们写书都是从行列式开始干，自学看书根本看不懂，当年线代上机考试之前三个小时还在玩魔兽世界🐶🐶🐶，这个故事告诉我们，出来混迟早要还的😂😂😂😂

用矩阵消元(Elimination Using Matrix)

本节的主要目的就是告诉你，小子，矩阵是用来解方程的，你会算行列式只能考上研究生，哈哈哈（博主吃不到狐狸说葡萄酸）
来个方程：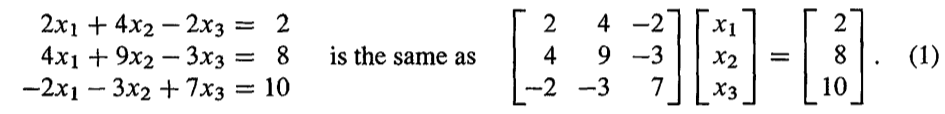

$$
\begin{bmatrix}x_1\\x_2\\x_3\end{bmatrix}
$$
是一个n维空间(space)，在这个空间里，我们找一个特定或者若干个特定的vector使得$ Ax=b $成立
根据row picture，和column pictur
:
$$
A\textbf{x}=col(1)x_1+rcol(2)x_2+\dots+col(n)x_n\\
$$
所以，Ax的第j行的元素结果是
$$
(A\textbf{x})_j=col(j,1)x_1+rcol(j,2)x_2+\dots+col(j,n)x_n\\
$$
观察上面的式子不难发现，Ax的第j个元素就是A的第j行和x的乘积
that is
$$
\sum_{j=i}^{n}a_{ji}x_i
$$
各位注意啦，这步放在这里主要是为了后面算矩阵乘以矩阵的，虽然看起来有点啰嗦，但是这样下来整个思路是完整的，不会出现漏洞

矩阵形式(Matrix form)

还是刚才说的，这节就是把消元的所有动作集成在一个矩阵里，我们的目的是
$$
A\textbf{x}=\textbf{b}\\
EA\textbf{x}=E\textbf{b}\\
U\textbf{x}=E\textbf{b}\\
$$
U是上三角矩阵
目标明确以后，对于上面的图片中的矩阵，我们开始消元，第一步， $(第二个方程)-2\times (第一个方程)$
得到的右侧b：

$$
b_{new}=\begin{bmatrix}2\\4\\10\end{bmatrix}\\
b_{new}=Eb
$$

没错我们关系E是个啥，先给出E，求解E的过程看后面。

$$
E=\begin{bmatrix}1& 0 & 0\\
-2 & 1& 0\\
0&0&1\end{bmatrix}
$$

算下Eb的结果，row picture或col picture给出的答案都是 $b_{new}$
不错，起码这个E是我们要找的变换矩阵。观察一下E，发现E是从$I$变形来的，把其中一个改成要乘以的那个系数的负数，比如我们要减去2倍的第一行，就把某个位置改成-2。但是具体改哪个位置是个关键：改的位置就是被减去的那一行的减去那一行的行的那一列，怎么样，迷糊没，迷糊就对了
E的第2行第1列是-2：我们要消去的是原矩阵A的第二行，的第一列元素

$$
Eb=b_{new}\\
\begin{bmatrix}
1&0&0\\
{-2}&1&0\\
0&0&1
\end{bmatrix}
\begin{bmatrix}
b_1\\
b_2\\
b_3
\end{bmatrix}
=\begin{bmatrix}
b_1\\
b_2-2b_1\\
b_3
\end{bmatrix}
$$

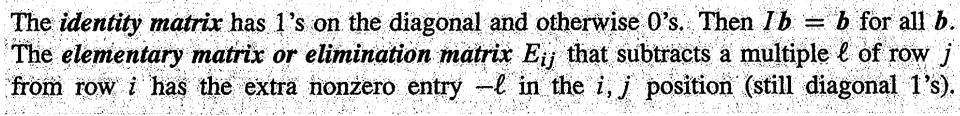
这个过程全靠自己领悟，如果这两种语言你都没明白，那就过几天再看一遍吧。

矩阵乘法(Matrix Multiplication)

我在考虑要不要新开篇，一想还是算了吧，新写一篇还要写开篇废话，麻烦死。
我们学会了矩阵乘以向量，那么矩阵乘以矩阵就是要解决上面那个EA的问题，
先说几个矩阵乘法的性质：
$$
A(BC)=(AB)C\\
often\;AB\not=BA\\
AB=A\begin{bmatrix}b_1&b_2&b_3\end{bmatrix}=\begin{bmatrix}Ab_1&Ab_2&Ab_3\end{bmatrix}
$$
这上面这个是乘法法则比较重要的一条，下一篇有详细介绍，包括乘法的具体算法，本篇只是大体观察一下乘法性质

交换行(Row Exchange)

Permutation Matrix也是从$I$演变出来的一种矩阵，其主要作用是交换矩阵的两行
eg：交换第二和第三行
$$\begin{bmatrix}1&0&0\\0&0&1\\0&1&0\end{bmatrix}\begin{bmatrix}1&2&3\\2&3&4\\3&4&5\end{bmatrix}=\begin{bmatrix}1&2&3\\3&4&5\\2&3&4\end{bmatrix}$$
没错，就这么神奇，不信自己慢慢算，交换可以用矩阵表示，之前的行之间的减法也可以用矩阵乘法，那么说Elimination基本可以用矩阵连续想成表示，比如我想消元之后再换行
$$
PEA=PEb
$$
这样就能得到一个可以back的upper triangular matrix了，或者更多的P和E。。。

增广矩阵(Augmented Matrix)

把b也放到A里面，放最后一列，那么矩阵就不是方阵了：
$$\begin{bmatrix}2&4&-2&2\\4&9&-3&8 \{-2}&-3&7&10\end{bmatrix}$$

conclusion

所以消元可以通过在A矩阵前面乘以一些列的变换，换行矩阵，得到最后的上三角矩阵
$$
U=P_nE_m\cdots P_2E_2P_1E_1A
$$
乘法的外表一些基本性质就是这些，我以为multiplication rule也在这一篇，原来不在，吓死我了，明天继续写，明天是个硬骨头，各位加油啊！