Abstract: 本文介绍正态分布第三部分,标准正态分布,正态分布的线性组合,对数正态分布以及对数正态分布
Keywords: The Normal Distributions,The Standard Normal Distribution
正态分布
废话就是概率论基础知识部分快要结束了,接下来的关于数理统计部分的内容很多都是依赖概率论的知识的,所以打好基础才好继续深入。
本文继续介绍标准正态分布,以及正态分布不同参数的比较。
标准正态分布 The Standard Normal Distribution
Definition Standard Normal Distribution.The normal distribution with mean 0 and variance 1 is called the standard normal distribution.The p.d.f. of the standard nromal distribution is usually denoted by the symbol $\phi$ ,and the c.d.f. is denoted by the symbol $\Phi$ .Thus,
$$
\phi(x)=f(x|0,1)=\frac{1}{(2\pi)^{1/2}}e^{-\frac{1}{2}x^2} \text{ for }-\infty<x<\infty
$$
and
$$
\Psi(x)=\int^{x}_{-\infty}\Psi(\mu)d\mu \text{ for }-\infty<x<\infty
$$
第二个公式中 $\mu$ 是个哑变量,根据微积分基本定理可以知道上面写的 c.d.f.的导数就是p.d.f.
正则化的本质就是均值为0,方差为1的正态分布被称为正态分布家族中的标准。
c.d.f是使用初等函数是无法求得的,也就是没有一个封闭的形式,就像本本节开始时说的,只能用查表或者数值法来求p.d.f的某段积分,或者查询c.d.f的结果做差得到对应段的p.d.f.
Theorem Consequences of Symmetry.For all x and all $0 < p < 1$
$$
\begin{aligned}
\Psi(-x)=1-\Psi(x)
\text{ and }
\Psi^{-1}(p)=-\Psi^{-1}(1-p)
\end{aligned}
$$
这个证明相对简单,其实主要考察的是上一篇关于正态分布的形状问题,正态分布p.d.f.的根本性质是对称性,关于均值对称,这个性质就可以衍生出上面定理的结论,比如 $Pr(X\leq -x)=Pr(X\geq x)$ 就是对称性质的体现,然后是c.d.f.的反函数重新改写前面这个对称性质,等是左边为 $\Psi^{-1}(\Psi(-x))=\Psi^{-1}(p)$ 以及 等式右边 $\Psi^{-1}(1-\Psi(x))=-\Psi^{-1}(1-p)$
Theorem Converting Normal Distributions to Standard.Let $X$ have the normal distribution with mean $\mu$ and variance $\sigma^2$ .Let $F$ be the c.d.f. of $X$ .Then $Z=(X-\mu)/\sigma$ has the standard normal distribution, and ,for all x and all $0 < p < 1$
$$
F(x)=\Phi(\frac{x-\mu}{\sigma})\\
F^{-1}(p)=\mu+\sigma\Phi^{-1}(p)
$$
这个定理要完成的一个任务是把一个一般的正态分布,通过随机变量的函数将原正态分布转换成标准正态分布,方法是目标随机变量减去均值后的差再除以标准差。
证明
$$
Pr(X\leq x)=Pr(Z\leq \frac{x-\mu}{\sigma})
$$
这就能得到结论了,令 $p=F(x)$ 能得到 $F^{-1}(p)=\mu+\sigma\Phi^{-1}(p)$ 的结论。
我们来举个计算的例子,我们来计算一个正态分布中的概率,假设X有一个正态分布,均值是5方差是2,我们来计算 $Pr(1<X<8)$
如果我们令 $Z=(X-5)/2$ 那么Z会有一个标准的正态分布并且:
$$
Pr(1<X<8)=Pr(\frac{1-5}{2}<\frac{X-5}{2}<\frac{8-5}{2})=Pr(-2<Z<1.5)\\
\text{futhermore:}\\
\begin{aligned}
Pr(-1<Z<1.5)&=Pr(Z<1.5)-Pr(Z\leq -2)\\
&=\Phi(1.5)-\Phi(-2)\\
&=\Phi(1.5)-[1-\Phi(2)]
\end{aligned}
$$
从书后标准正态分布的表格中可以查到c.d.f.为 $\Phi(1.5)=0.9332$ 并且 $\Phi(2)=0.9773$ 所以
$$
Pr(1<X<8)=0.9105
$$
本section的精髓是,首先我们没办法计算正态分布的不定积分,所以想求值要查表,查表你有不能对每一个分布参数都建表,所以要制造一个标准,其他的不同参数和标准有数字关系,于是定义一个标准正态分布,然后所有正态分布和标准正态分布产生数字联系,就能用一张表解决问题了。
正态分布比较 Comparisons of Normal Distributions
接着我们来比较一下,不同参数的正态分布。得到的结论是均值决定了位置,方差决定了胖瘦。
这里有一个非常重要的性质,以均值位置为参考物,一个标准偏移是一个标准差,这个偏移之内的概率是相等的,并且任意个相同的标准偏移都相等,对于两个正态分布有$f_1(X|\mu_X,\sigma_X^2),f_2(Y|\mu_Y,\sigma_Y^2)$ 有正数 $k$ :
$$
Pr(\mu_X-k\sigma_X<X<\mu_X+k\sigma_X)=Pr(\mu_Y-k\sigma_Y<Y<\mu_Y+k\sigma_Y)
$$
另一种直观的方式是所有正态分布和标准正态分布进行比较,那么就有
$$
p_k=Pr(|X-\mu|\leq k\sigma)=Pr(|Z|\leq k)
$$
如图: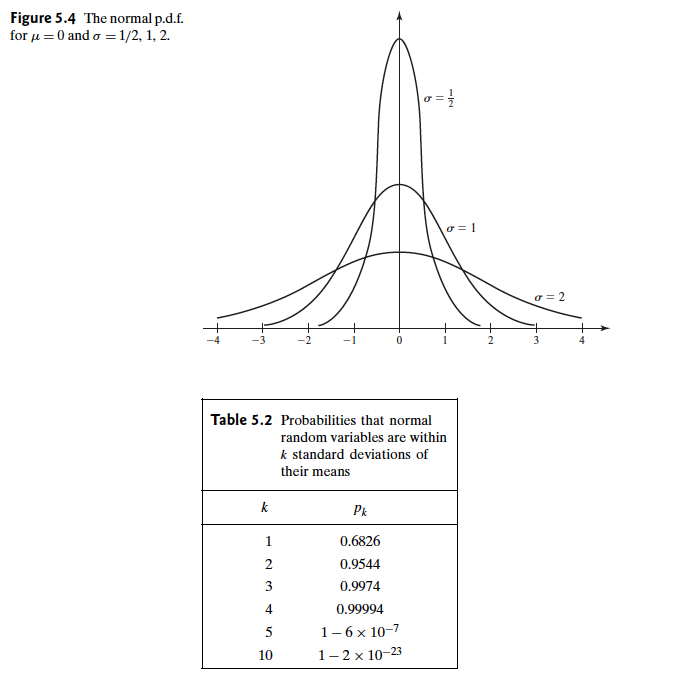
表格中k表示几个标准偏移,也就是k的具体值,可以看出,当$k=3$ 的时候,正态分布内 $Pr(\mu-3\sigma,\mu+3\sigma)>0.99$ 了而且我记得我大学书上有个 $3-\sigma$ 原则,好像是当检测结果满足这个要求的时候就算合格了,这个具体的我们在数理统计部分再说,我们要知道的是正态分布的形状,和偏移性质。
正太分布随机变量的线性组合 Linear Combinatios of Normally Distributed Variables
在经过标准化变换后我们思考的另一个问题,就是多个正态分布的随机变量的线性组合会是什么样子呢?
Theorem If the random variables $X_1,\dots,X_k$ are independent and if $X_i$ has the normal distribution with mean $\mu_i$ and variance $\sigma^2_i(i=1,\dots,k)$ ,then the sum $X_1+\dots+X_k$ has the normal distribution with mean $\mu_1+\dots+\mu_k$ and variance $\sigma^2_1+\dots+\sigma^2_k$
定理是说,如果把几个正态分布的独立随机变量加起来得到的随机变量也是正态分布的,并且均值是原来随机变量的均值的和,方差也是原随机变量的方差的和。
证明:
使用强有力的工具m.g.f.
用 $\Psi_i(t)$ 表示 第 $X_i$ 的m.g.f. $(i=1,2,\dots)$ 然后用 $\Psi(t)$ 表示 $X_1+\dots+X_k$ 的m.g.f.
$$
\Psi(t)=\Pi^{k}_{i=1}\Psi_i(t)=\Pi^k_{i=1}exp[\mu_it+\frac{1}{2}\sigma^2_it^2]\\
=exp{[(\sum^k_{i=1}\mu_i)t+\frac{1}{2}(\sum^{k}_{i=1}\sigma^2_i)t^2]}
$$
直接就能得到我们想要的结论,可见m.g.f.大法好。
Corollary If the random variables $X_1,\dots,X_k$ are independent,if $X_i$ has the normal distribution with mean $\mu_i$ and variance $\sigma^2_i (i=1,\dots,k)$ ,and if $a_1,\dots,a_k$ and $b$ are constants for which at least one of the values $a_1,\dots,a_k$ is different from 0,then the variable $a_1X_1+\dots+a_kX_k+b$ has the normal distribution with mean $a_1\mu_1+\dots+a_k\mu_k+b$ and variance $a_1^2\sigma_1^2+\dots+a^2_k\sigma_k^2$
线性组合的推论,证明方法和上面定理一致,使用m.g.f.可以很轻松的得到。
Definition Sample Mean.Let $X_1,\dots,X_n$ be random variables,The average of these $n$ random variables $\frac{1}{n}\sum^{n}_{i=1}X_i$ ,is called their sample mean and is commonly denoted $\bar{X}_n$
有n个随机变量,他们的均值,被称为样本均值,记做 $\bar{X}_n$ 注意,这里并没有说 $X_i$ 的分布和独立性关系。也就是说是任意的的分布都可以。
Corollary Suppose that the random variables $X_1,\dots,X_n$ form a random sample from the normal distribution with mean $\mu$ and variance $\sigma^2$ ,and let $\bar{X}_n$ denote their sample mean .Then $\bar{X}_n$ has the normal distribution with mean $\mu$ and variance $\sigma^2/n$
上面定义的一个推论,是否成立呢?我们来证明一下,用什么证明呢?我们的线性性质就能证明这一点:
$$
\bar{X}_n
=\sum^{n}_{i=1}(1/n)X_i
$$
这就是一个线性组合,而且根据条件,$X_i$ 的均值方差一致,那么均值最后不变 $\sum^n_{i=1}\frac{1}{n}\mu_i=\mu_i$ 而对应的方差应该是 $\sum^{n}_{i=0}\frac{1}{n^2}\sigma^2=\sigma^2/n$
证毕
正态分布的对数 The Lognormal Distributions
对数正态分布,就是对随机变量进行一个对数变换后,这个新的分布是正态分布。
Definition Lognormal Distribution.If $log(X)$ has the normal distribution with mean $\mu$ and variance $\sigma^2$ ,we say that $X$ has the lognormal distribution with parameters $\mu$ and $\sigma^2$
我们之前研究的都是一个某分布的随机变量经过一个函数变换后产生新的随机变量对应的分布是什么样的,今天是反过来,一个随机变量经过函数变换后是正态分布,那么这个分布是怎么样的。
总结
本文主要介绍了正态分布的形状,和不同正态分布之间的相关性一致性,以及正态分布随机变量的线性组合结果,以及扩展的对数正太分布,可以看出正态分布有很多非常简单有用的性质。
下一篇我们进入gamma分布。。。
