Abstract: 本文介绍继期望之后分布的另一个重要数学性质,方差
Keywords: Variance,Standard Deviation
方差
这两天更新有点频繁,但是没办法,必须快速的完成的基础知识积累,毕竟时间是有限的,还要留出更多的时间用于更进一步的深入研究,打牢基础的同时尽可能的提升速度。
如果我虚度光阴,那就请结束我的一生。如果你用奉承掐媚愚弄我,那我便自得取乐,如果你用荣华富贵诱惑我,那即便我的末日来临,我也要赌个输赢!
虽然期望很有用,但是并不能够完全的反应分布的信息,这么思考,首先,一个分布是一个公式确定的,这个公式的结构,和参数,如果能用一个参数全部概括,那么我们就有了一个超级模型一样的东西,这显然是不存在的,所以我们要用更多的数字特征来描述,代表一个分布的样子。
本文我们就介绍一款特征可以表示分布的离散程度(英文叫 “spread out”)——方差,他的衍生小弟叫做标准差是他的平方根,目前还不知道有啥特殊用途。
先举个例子,股票。。
一个股波动范围在 $[25,35]$ 之间,均匀分布,第二个股分布在 $[15,45]$ 之间的均匀分布。
那么其图像显示如下:
可见这个图像上,均值一致,都是30,但是分布有着明显区别,我们开始介绍我们的主角——“方差”
方差和标准差的定义 Definitions of the Variance and the Standard Deviation
Definition Variance/Standard Deviation.Let $X$ be a random variable with finite mean $\mu=E(X)$ ,The variance of $X$ denoted by $Var(x)$ ,is defined as follows:
$$
Var(X)=E[(X-\mu)^2]
$$
上面是关于方差和标准差的定义,首先随机变量的必须有一个有限的期望,然后再这个期望的基础上,每个变量和均值做差然后求其平方的期望,一共两步,用到了两次期望,可见方差其实就是随机变量函数的期望,而这个函数内又包含期望的运算。
注意无限的均值,或者不存在均值,都会导致方差无法计算,这是我们说随机变量没有方差,比如柯西分布,没有均值,也就没有方差,可见不是所有分布都有均值和方差的,同样,后面所有用到期望求的数字特征都没有。
方差用希腊字母 $\sigma^2$ 表示,标准差用希腊字母 $\sigma$ 表示,这是单个变量的分布时,当有多个变量的时候只需要对$\sigma$ 加以区分就可以,比如加下标 $\sigma_a$ so so
那么我们来计算个🌰 :
计算上面例子中第一种股票的方差:
在$[25,35]$ 的均匀分布
$$
Var(A)=\int^{35}_{25}(a-30)^2\frac{1}{10}da=\frac{1}{10}\frac{x^3}{3}\arrowvert^5_{x=-5}=\frac{25}{3}
$$
上面的积分,和积分限的计算请自行打草稿,这里不再赘述了。
下面开始看看方差有哪些定理
Theorem Alternative Method for Calculating the Variance.For every random variable $X$ , $Var(X)=E(X^2)-[E(X)]^2$
这个定理中文不知道叫啥,二选一定理?不知道,反正结论是方差可以直接用两个期望计算,一个是随机变量的平方的期望,另一个是期望的平方。
证明:
$$
\begin{aligned}
Var(X) & =E[(X-\mu)^2]\\
& =E(X^2-2\mu X+\mu^2)\\
& =E(X^2)-2\mu E(X)+ \mu^2\\
& =E(X^2)-\mu^2
\end{aligned}
$$
Q.E.D
简单的计算过程,用到的性质都是期望的性质,所以又不懂回到前两篇重新研究。
方差和标准差只取决于其分布,而且其实际意义就是随机变量对均值 $\mu$ 的离散程度,值越大说明越分散,相反,越小表示与均值越聚集。
这里可以有个例子,这里我就不写啦,大家自己看书吧
方差的性质 Properties of the Variance
学了定义,该学性质了,看起来方差的性质没有期望多,期望用了整整一课来说明,方差只是一个小section。
Theorem For each $X$ , $Var(X)\geq 0$ .If $X$ is a bounded random varibale,then $Var(X)$ must exist and be finite.
对于所有随机变量,其方差永远是大于等于零的,其为0的情况是当且仅当, $Pr(X=\mu)=1$
如果 随机变量 $X$ 有界,那么其方差必然存在,并且是有限的。
这个定理的证明要靠概念,没有逻辑过程,首先根据定义,方差是个平方,所以其必然大于等于0,又因为方差存在与否取决于两个期望,如果这两个期望都存在,方差没有不存在的理由,故而有界随机变量存在期望,故成立,证毕。
Theorem $Var(X=0)$ if and only if there exists a constant c such that $Pr(X=c)=1$ ,then $\mu=c$ and $Pr[(X-c)^2=0]=1$
哈哈,刚才一不小心把这个定理先直播出来了,那么我们就直接证明,证明 if and only if 要证明两个方向:
假设存在一个随机变量 $X$ 和一个常数c 满足 $Pr(X=c)=1$ 那么 $E(X)=c$ 并且 $Pr[(X-c)^2=0]=1$ 然后就有了
$$
Var(X)=E[(X-c)^2]=0
$$反过来假设 $Var(X)=0$
- 那么就有 $Pr[(X-\mu)^2\geq 0]=1$ 。
- 但是又因为 $E[(X-\mu)^2]=0$ 也就是 $0=\int^{\infty}_{-\infty}Pr【(x-\mu)^2】(x-\mu)^2dx$
- 根据定理( Theorem Suppose that $E(x)=a$ and that either $Pr(X\geq a)=1$ or $Pr(X\leq a)=1$ Then $Pr(X=a)=1$)
- 可以得到
$$
Pr[(X-\mu)^2=0]=1
$$
证毕(其实2中用的那个定理有点问题,我还没想明白)
Theorem For constant $a$ and $b$ let $Y=aX+b$ Then
$$
Var(Y)=a^2Var(X)
$$
and $\sigma_Y=|a|\sigma_X$
定理表明线性关系下,随机变量的方差的变化
证明:令 $\mu=E(X)$ 那么根据上一篇我们有 $E(Y)=aE(X)+b$
$$
\begin{aligned}
Var(Y) & =E[(aX+b-a\mu-b)^2]=E[(aX-a\mu)^2]\\
& =a^2E[(X-\mu)^2]=a^2Var(X)
\end{aligned}
$$
求平方根就能得到关于标准差的公式。
当线性变换中 $a=1$ 的时候就变成给分布搬家了,而其形状完全不变: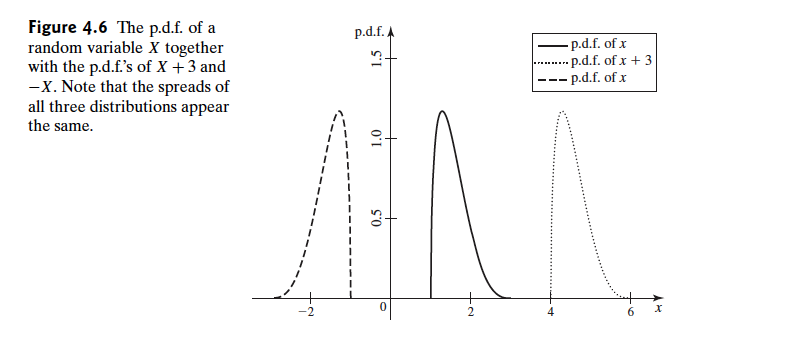
图上就是搬家计算了,图例中最后一个是错的,应该是 $x-3$
根据上面定理还能推导出一些其他关系式,比如说:
$$
Var(-x)=Var(x)
$$
Theorem If $X_1,\dots,X_n$ are independent random variable with finite means,Then
$$
Var(X_1+\dots +X_n)=Var(X_1)+\dots+Var(X_n)
$$
独立随机变量之和的方差等去其方差之和,证明过程如下:
证明:
我们只证明两个独立随机变量的情况
假设 $E[X_1]=\mu_1$ 以及 $E[X_2]=\mu_2$ 然后有
$$
E[X_1]+E[X_2]=\mu_1+\mu_2
$$
那么
$$
\begin {aligned}
Var(X_1+X_2)& =E[(X_1+X_2-\mu_1-\mu_2)^2]\\
&=E[(X_1-\mu_1)^2+(X_2-\mu_2)^2+2(X_1-\mu_1)(X_2-\mu_2)]\\
&=E[(X_1-\mu_1)^2]+E[(X_2-\mu_2)^2]+E[2(X_1-\mu_1)(X_2-\mu_2)]\\
&=Var(X_1)+Var(X_2)+E[2(X_1-\mu_1)(X_2-\mu_2)]
\end{aligned}
$$
根据随机变量期望的性质
$$
\text{When } X_1 \text{ and } X_2 \text{ are independent}\\
E[2(X_1-\mu_1)(X_2-\mu_2)]=2\times E[(X_1-\mu_1)]E[(X_2-\mu_2)]=0
$$
证毕
这就是关于独立随机变量方差之间的关系,但是如果不是独立的随机变量,他们的方差会是什么样的呢?这是个很有意思的课题,后面我们会介绍相关话题。
Corollary If $X_1,\dots,X_n$ are independent random varibales with finite means,and if $a_1,\dots,a_n$ then
$$
Var(a_1X_1+\dots+a_nX_n)=a^2Var(X_1)+\dots+a_n^2Var(X_n)
$$
这个推论的证明用到了上面两个已经被证明的定理,所以我们就不用证明了,没错,我又开始偷懒了。。
二项分布的方差 The Variance of a Binomial Distribution
二项式分布的方差:
独立同伯努利分布的随机变量的和是满足二项分布的随机变量,这个我们前面已经说过了,后面下一章还会再说,我们现在就假装知道他们是独立的就行,根据独立随机变量的方差性质。
$$
Var(X)=\sum^{n}_{i=1}Var(X_i)
$$
然后我们根据二选一定理,某个伯努利随机变量 $Var(X_i)=E(X_i^2)-[E(X_i)]^2$ 来计算方差,首先要得到 $X_i^2$ 的方差,因为伯努利分布只有0和1,那么$X_i^2$ 也是0和1,故 $X_i^2$ 的分布于原始 $X_i$ 的分布一样,均值是 $p$ (参考不努力分布的期望)那么,我们就有
$$
Var(X_i)=E(X_i^2)-[E(X_i)]^2=p-p^2
$$
这是对于某一个随机变量的方差,因为他们互不相关,所以把他们加起来就好了,最后结果:
$$
\begin{aligned}
Var(X) & =\sum^{n}_{i=1} Var(X_i)\\
& =\sum^{n}_{i=1}(p-p^2)\\
&=np(1-p)
\end{aligned}
$$
行了,就这么样了,二项分布的方差就是上面这个了。
四分位数范围 Interquartile Range
我们是否还记得方差的实际意义,他描述的是分布距离均值的离散程度,方差可以没有,也就是说当期望不存在或者无限的时候,方差可以不存在,但是描述分布的离散程度,这个可以有啊,所以我们就提出个新的数字特征,这个特征能帮忙解决没有方差,比如柯西分布,这种特殊的分布的离散程度的刻画。
Definition Interquartile Range(IQR). Let X be a random varibale with quatile function $F^{-1}(p)$ for $0<p<1$ .The interquartile range (IQR) is defined to be $F^{-1}(0.75)-F^{-1}(0.25)$
换句话说,IQR就是四分之一分位数,和四分之三分位数之间的距离。
总结
继期望过后,我们用期望引申出了一个更复杂的,刻画分布另一个性质的期望。
下几篇还是期望,我们本章就叫期望。
待续
