Abstract: 本文承接上文,对于二维联合分布,如何求出二维变量中一个变量的一个分布,也就是标题所说的边缘分布;以及对独立随机变量的讨论。
Keywords: Marginal p.f.,Marginal p.d.f.,Independent
边缘分布
今天这篇可能是农历新年前最后一篇关于数学的博客了,过年期间争取把CUDA系列的写出来,大家有兴趣的可以关注一下,过年本来是个休息的时间,但是说实话,现在真的很讨厌过年,尤其是那些关心你生活的所谓亲戚们,可能是变向找平衡,或者是炫耀,具体案例我不说,已经烂大街了,只是觉得有点恶心,人们在内心是相互攀比相互较量,表面还要装作一团和气,然后各种映射暗示你不如他的地方。
过年就应该是一家团聚,相互祝福,相互鼓励的。
真的想找个没人的地方看一春节书,改变不了就是试着逃避吧。
想要逃出生天,好好学习,可能还有机会。
边缘分布 Marginal Distribution
我们继续我们的概率论,我们已经经历了概率论的变化过程是:从试验到样本空间,样本空间到事件,事件到概率(复合事件的概率,包括条件事件,独立事件等等扩展情况),样本空间到随机变量,随机变量的离散概率、连续概率,描述随机变量概率的工具(p.f.,p.d.f.,c.d.f.),然后随机变量被扩展为二维(离散的,连续的,混合的),今天我们在二维联合分布的情况下,推出今天的主要讨论目标:Marginal Distribution(边缘分布)
上文我们曾有一个小伏笔,我们想知道联合的p.f.或者p.d.f.怎么通过每个变量的p.f.或者p.d.f.求出的;或者我们反过来,如何通过联合的p.f.或者p.d.f.来得到每个变量自己的(一维的)p.f.或者p.d.f.。
这就是我们要说的今天的边缘分布,适用于p.d.f.或者p.d.或者c.d.f.
求边缘概率(分布)函数 Deriving a Marginal p.f. or a Marginal p.d.f.
离散分布边缘概率函数 Discrete
首先我们来从简单的二维联合分布来看,从有限的离散二维联合分布,举个🌰 :
对于一个二维分布,上文说得到的扔骰子和丢硬币,下面我们的例子硬币和骰子都不是均匀的,所以产生的概率分布与原始例子不太一样:
| Head | Tail | $f_1(x)$ | |
|---|---|---|---|
| 1 | $\frac{1}{24}$ | $\frac{3}{24}$ | $\frac{1}{6}$ |
| 2 | $\frac{2}{24}$ | $\frac{2}{24}$ | $\frac{1}{6}$ |
| 3 | $\frac{3}{24}$ | $\frac{1}{24}$ | $\frac{1}{6}$ |
| 4 | $\frac{1}{24}$ | $\frac{3}{24}$ | $\frac{1}{6}$ |
| 5 | $\frac{1}{24}$ | $\frac{3}{24}$ | $\frac{1}{6}$ |
| 6 | $\frac{2}{24}$ | $\frac{2}{24}$ | $\frac{1}{6}$ |
| $f_2(y)$ | $\frac{5}{12}$ | $\frac{7}{12}$ | 1 |
陈希孺先生在书中说,简单的来说,边缘概率就是上面这个表的边缘,下面的一行,右边的一列所表现出来的分布,下面的一行,就是变量y,试验(丢硬币的)的边缘分布,对应的右侧一列对应的是随机变量x对应的试验是扔骰子。
Definition Marginal c.d.f./p.f./p.d.f. Suppose that X and Y have a joint distribution.The c.d.f. of X derived by theorem 3.4.5. is called the marginal c.d.f. of X.Similarly,the p.f. or p.d.f. of X associated with the marginal c.d.f. of X is called the marginal p.f. or marginal p.d.f. of X
写书的好处就是可以省略掉很多前面已经写了的东西,然后一个指针指过去就可以了,写博客也可以,就像这样3-4,但是我们还是重写一遍定理3.4.5:
Theorem Let $X$ and $Y$ have a joint c.d.f. $F$.The c.d.f. $F_1$ of just the single random variable $X$ can be derived from the joint c.d.f. $F$ as $F_1(x)=lim_{y\to \infty}F(x,y)$.Similarly,the c.d.f. $F_2$ of $Y$ equals $F_2(y)=lim_{x\to \infty}F(x,y)$ ,for $0<y\leq \infty$
定义3.4.5告诉我们如何把一个联合c.d.f.拆分出来,通过把一个变量写成无穷大,来得到另一个变量的c.d.f.,这个过程就是一个边缘c.d.f.的过程,对于p.f.和p.d.f.同样的操作得到的将会是边缘p.f.或者边缘p.d.f.
那么我们怎么得到边缘p.f.或者边缘p.d.f呢?
Theorem If $X$ and $Y$ have a discrete joint distribution for thich the joint p.f. is $f$,then the marginal p.f. $f_1$ of $X$ is
$$
f_1(x)=\sum_{\text{All } y}f(x,y).
$$
Similarly,the marginal p.f. $f_2$ of $Y$ is
$$
f_2(y)=\sum_{\text{All } x}f(x,y).
$$
这个定理可以用来计算一个二维离散随机变量的联合分布如何计算出两个离散变量分别的离散分布,而书上给出的证明也过于感性化,作者通过一副和我们上一篇类似的图来说明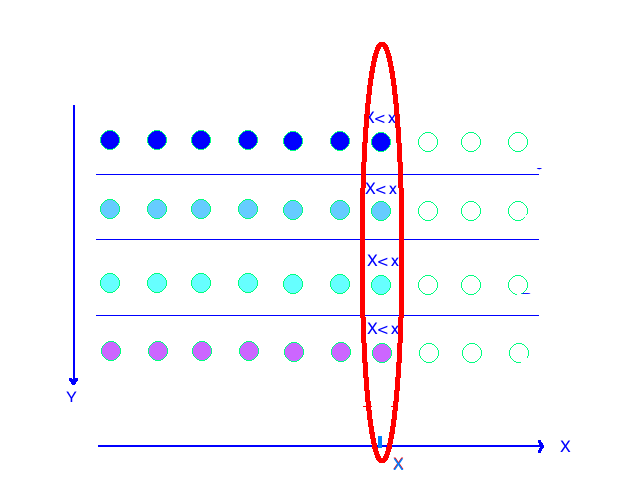
$f_1(x)$ 是在联合分布概率函数中,某一个变量不变($x$) 而另一个变量取和的这种方式,来得到的边缘分布(x的一个一维分布概率函数)。如果从最初的关于概率的定义出发,我们也能得到类似的结论,二维随机变量对应的可以能是一个试验的二维结果,二维结果就对应了两个维度的可能性,而这个二维联合p.f.就是描述这个二维结果发生的概率的,当一个维度的可能性被消除(也就是二维变一维:$(x,y)\to x$)那么就应该把同一个 $x$ 下的所有不同的 $y$ 都加起来,因为在二维联合分布情况下 $(x_i,y_k)$ 和 $(x_i,y_l)$ 是不相关的($k\neq l$)所以可以进行加法。
连续分布边缘概率密度函数 Continuous
接着我们看连续情况下的:
Theorem If X and Y have a continuous joint distribution with joint p.d.f $f$ then the marginal p.d.f. f_1 of X is
$$
f_1(x)=\int_{-\infty}^{\infty}f(x,y)dy \text{ for }-\infty<x<\infty
$$
Similarly,the marginal p.d.f.f_2 of Y is
$$
f_2(y)=\int_{-\infty}^{\infty}f(x,y)dx \text{ for }-\infty<y<\infty
$$
这个证明方法有点意思,用到了c.d.f.的定义和c.d.f.的边缘分布的定义,我们假设这个二维连续联合分布的p.d.f是$f(x,y)$ 那么根据c.d.f.的定义$F(x,y)$ 为下面的式子:
$$
F(x,y)=\int^{x}_{-\infty}\int^{y}_{-\infty}f(x,y)dydx
$$
没问题,当我们想得到x的边缘c.d.f.,我们根据定理,要把$y\to \infty$
$$
F(x)=\int^{x}_{-\infty}\int^{\infty}_{-\infty}f(x,y)dydx
$$
F(x)和$f(x)$ 是导数与反导数的关系,所以,F(x) 求导可以得到:
$$
f(x)=\frac{dF(x)}{dx}=\frac{d\int^{x}_{-\infty}\int^{\infty}_{-\infty}f(x,y)dydx}{dx}\\
\text{set :}\int^{x}_{-\infty}[\int^{\infty}_{-\infty}f(x,y)dy]dx=\int^{x}_{-\infty}g(x)dx\\
\text{so }f(x)=g(x)=\int^{\infty}_{-\infty}f(x,y)dy
$$
Q.E.D
证明过程用到了单变量c.d.f.和p.d.f.之间的关系,上面提到的定理3.4.5(莫名其妙的编号来自原书),以及微积分基本定理,这个证明过程如上所述,简单粗暴(与书本给出的证明不太一样,如有问题请及时指出,谢谢)。
有了上面这些个公理,使用过程多半就变成了春计算,公理背后的逻辑就是上面我们的两个证明,一个图解,一个分析,虽然不太喜欢做计算,但是我们还是写个例子吧:
假设一个二维联合分布满足:
$$
f(x,y)=
\begin{cases}
\frac{21}{4}x^2y&\text{for }x^2\leq y\leq 1\\
0&\text{otherwise}
\end{cases}
$$
求 $x$ 的边缘p.d.f.
$$
f_1(x)=\int^{\infty}_{-\infty}f(x,y)dy=\int^{1}_{x^2}\frac{21}{4}x^2ydy=(\frac{21}{8})x^2(1-x^4)
$$
混合分布 Mixed
Theorem Let f be the joint p.f./p.d.f. of X and Y,with X discrete and Y continuous.Then the marginal p.f. of X is :
$$
f_1(x)=Pr(X=x)=\int^{\infty}_{-\infty}f(x,y)dy \quad\text{for all }x
$$
and the marginal p.d.f. of Y is:
$$
f_2(y)=\sum_{x}f(x,y) \text{ for }-\infty<y<\infty
$$
证明就是前两个的集合版本。例子也不再废话了,也是上面两个例子的结合,我们要进入下面这个比较重要的主题了,关于随机变量的独立性。
随机变量的独立 Independent Random Variables
我们前面研究过事件的独立性,事件独立不是不相关,而是其概率满足一定关系,我们称之为独立,也就是事件发生与否不会影响另一个事件,我们称之为相互独立,而我们通过随机变量把样本空间(也包括事件)过渡到实数,那么这些实数之间的概率相互独立是怎么回事呢?
对于离散随机变量,其独立性和事件的独立性非常相似:
$$
Pr((x,y))=Pr(x)Pr(y)
$$
但是对于连续变量,这个就有问题了,因为连续变量的单一位置的概率是0,中已经做了明确的介绍,所以我们要有一片区域代替一个点。
先来看一个总体的定义:
Definition Independent Random Variables.It is said that two random variables $X$ and $Y$ are independent if,for every two sets $A$ and $B$ of real numbers such that ${x\in A}$ and ${Y\in B }$ are events,
$$
Pr(X\in A \text{ and } Y \in B)=Pr(X\in A)Pr(Y\in B)
$$
从事件的角度去看这个定义很明确了我们假设事件 $E={X\in A}$ 事件 $F={Y\in B}$ 这两个事件独立的条件是当且仅当:
$$
Pr(E\cap F)=Pr(E)Pr(F)
$$
上面的定义并没有规定A和B的选择方法,那么我们可以规定如下的规则:
$$
Pr(X\in{X<x})\\
Pr(Y\in{Y<y})\\
\text{so we have:}\\
Pr(X\leq x\text{ and }Y\leq y)=Pr(X\leq x)Pr(Y\leq y)
$$
哈哈哈,看出来上面藏了个谁了么?没有?仔细看?还没有?再仔细看。
判定随机变量独立方法 1
Theorem Let the joint c.d.f. of $X$ and $Y$ be $F$ let the marginal c.d.f. of $X$ be $F_1$ and let the marginal c.d.f. of $Y$ be $F_2$ Then $X$ and $Y$ are independent if and only if ,for all real numbers $x$ and $y$ ,
$F(x,y)=F_1(x)F_2(y)$
怎么样,加上这个定理是不是明显一点了呢?
于是我们得到了一个确定随机变量是否独立的方法,随机变量独立的充分必要条件就是其c.d.f.满足乘法关系,怎么来的?随机变量独立的定义在上面规定的。
判定随机变量独立方法 2
上面的定理很简单,不需要解读,我们继续看下面的定理通过joint p.d.f., joint p.f. 或者是joint p.f./p.d.f. 确定随机变量独立:
Theorem Suppose that $X$ and $Y$ are random varibales that have a joint p.f.,p.d.f. or p.f./p.d.f. $f$ ,Then $X$ and $Y$ will be independent if and only if $f$ can be represented in the following form for $-\infty<x<\infty$ and $-\infty<y<\infty$ :
$$
f(x,y)=h_1(x)h_2(y)
$$
这个定理给出了用pdf或者pf或者混合pf和pdf确定随机变量独立的方法,我们这里证明最复杂的情况,一个是离散的随机变量x,一个是连续的随机变量y,证明过程分为两部分,
- “if” part:
$$
\text{ hold: } f(x,y)=h_1(x)h_2(y) \\
\text{marginal p.d.f. of }x\text{ : }f_1(x)=\int^{\infty}_{-\infty}h_1(x)h_2(y)dy=c_1h_1(x)
$$
$c_1$ 是一个非负函数积分的结果,所以我们保证其是非负数,同时我们确定其有限,并且不是0,那么我们就能得到:
$$
h_1(x)=\frac{f_1(x)}{c_1}
$$
与此相似,我们用求和的方法求离散的边缘分布:
$$
f_2(y)=\sum_{x}f(x,y)=\sum_{\text{All }x}h_1(x)h_2(y)=h_2(y)\sum_{x}\frac{1}{c_1}f_1(x)=\frac{1}{c}h_2(y)
$$
我们分别求出了两个随机变量的概率密度函数和概率函数(这两个函数具有任一性,也就是可以代表整个pdf或者pf族),所以我们可以得到结论:
$$
f(x,y)=\frac{f_1(x)}{c_1} c_1 f_2(y)=f_1(x)f_2(y)
$$
结合我们关于随机变量的定义(mixed 版本):
$$
Pr(X\in A \text{ and } Y \in B)=\sum_{X \in A}\int_Bf(x,y)dy\\
=\int_B\sum_{X\in A}f_1(x)f_2(y)dy=\sum_{X\in A}f_1(x)\int_Bf_2(y)dy
$$
所以根据定义,随机变量独立!
- “only if” part:
we assume that X and Y are independent:
$$
Pr(X\in A \text{ and } Y \in B)\\
=\sum_{X\in A}f_1(x)\int_Bf_2(y)dy\\
=\int_B\sum_{X\in A}f_1(x)f_2(y)dy
$$
经过上面的分解,我们就能得到两个随机变量的概率
$$
Pr(A)=h_1(x)=\sum_{X\in A}f_1(x)\\
Pr(B)=h_2(y)=\int_Bf_2(y)dy
$$
这部分证明过程用到了上一篇混合随机变量的联合概率密度函数( $Pr(X\in A \text{ and } Y \in B)=\sum_{X\in A}f_1(x)\int_Bf_2(y)dy$ ) 然后通过微积分的基本过程得到了结论
Q.E.D
所以我们在平时思考的时候,当我们考虑两个随机变量是否独立的时候,只要思考当一个概率密度函数(概率函数)从未知变成已知的时候时,另一个是否受到影响,反之亦然。
举个例子:
假设两个连续变量满足如下分布
$$
f(x,y)=
\begin{cases}
kx^2y^2&\text{for }x^2+y^2\leq 1\\
0&\text{otherwise}
\end{cases}
$$
X,Y是否独立。
明显这个是不独立的,为啥,我们发现,$f_1(0.9)\neq 0$ 而 $f_2(0.9)\neq 0$ 但是
$f_1(0.9)f_2(0.9)=0$
所以我们可以确定其并不独立。
我们看出这个例子的定义域是个圆心在原点,半径为1的圆,那么这个定义域和独立与否是否有关系呢?
于是我们引出下面的定理:
判定随机变量独立方法 3
Theorem Let $X$ and $Y$ have a continuous joint distribution .Suppose that ${(x,y):f(x,y)>0}$ is a rectangular region $R$ (possibly unbounded) with sides (if any) parallel to the coordinate axes.Then X and Y are independent if and only if $f(x,y)=h_1(x)h_2(y)$ holds for all $(x,y)\in \Re^2$
这个定理对于上面例题是个很好的总结,当随机变量范围不是一个边和数轴平行的矩形时(有无边界无所谓,也就是开区间还是闭区间无所谓)没有可能独立,肯定相关,只有当其实矩形的时候,才有可能是独立的,是矩形,同时满足上面的给出的判断定理,就能确定是否独立了。
这个可以看做一个判定方法,也可以说是2的一个扩展
判定随机变量独立方法 4
对于形式上就是分离的函数,其随机变量独立:
$$
f(x,y)=e^xy\quad \text{ for } -\infty<x<0 \text{ and }0<y<1
$$
这个x和y的函数可以一眼就分离开了,同时定义域是矩形,而且积分是1(我自己编的例子,有问题请留言)
从定义上证明也很好证明,我们的定义是:
$$
Pr(X\in A \text{ and } Y \in B)=Pr(X\in A)Pr(Y\in B)
$$
那么我们就把事件A设置成 $Pr(A)=e^x$ 事件B设置成 $Pr(B)=y$ 这就明显了,
$$
Pr(X\in {X<e^x} \text{ and } Y \in {Y<y})=e^xy
$$
总结
本文知识点主要在随机变量的独立上,边缘概率比较直观,后面的条件概率和边缘概率有点相似,但是更复杂更有用一些,我们年后继续,祝大家新年快乐!
待续。。。。。
