Abstract: 本文主要介绍双变量的分布情况,以及其中的一些有用的性质
Keywords: Discrete Joint Distribution,Continuous Joint Distribution,Mixed Bivariate Distribution,Bivariate Cumulative Distribution Functions
二维分布
今天的废话还是想劝诫自己也劝诫那些看过我的博客和希望学有所成的人,学习也好,开发也好,投资也好,最忌急功近利,想一年翻十倍,有可能,但是概率小到报表,到后面学到具体的一些分布的时候,就知道这个方差有多大,人生需要经历,经历了就明白了,感谢周围所有的人,帮助过我们的,让我们受到人们,他们做的所有都在促进我们成长,一步一个脚印,慢就是稳,稳就是快。
本文我们介绍两个变量的分布,数学的两大分支,理论数学和应用数学,这两者没有明确的界限,不管什么理论,只有应用了以后才能推动社会进步,同时存进新的理论形成,所以,两者没有什么主次,都是重要的,概率论的应用性极强,我们不断学习,知识逐渐变得复杂,这个目的不是为了复杂而复杂,而是为了接近真相,我们生活中很少简单单变量的事件,出了扔硬币,甚至中国国粹打麻将扔骰子都是一次扔两个,那么就有了两个随机变量组合的问题,当然你也可以发明一个一边扔骰子一边扔硬币的游戏。
我们不断地复杂模型,就是为了去更好的描述实际情况,而简单的模型所能模拟的情况,多半是我们自己为了附会模型而创造的。
联合分布 Joint Distribution
对于双变量,我们有下面这些组合:
$$
\text{Bivariate}=
\begin{cases}
Discrete & \text{Discrete,Discrete}\\
Continuous & \text{Continuous,Continuous}\\
Hybrid & \text{Discrete,Continuous}
\end{cases}
$$
学习概率从一开始我们就是按照先离散后连续的方式逐步进行,像上台阶一样,那么我们二维随机变量也从离散开始。
Definition Joint/Bivariate Distribution:Let $X$ and $Y$ be random varibales.The joint distribution or bivariate distribution of $X$ and $Y$ is the collection of all probabilities of the form $Pr[(X,Y)\in C]$ for all sets $C$ of pairs of real numbers such that ${(X,Y)\in C}$ is an event
再次回忆随机变量(函数),和样本空间(集合)之间的关系,随机变量是一个函数,把样本空间上的样本点映射到实数,那么如果有两个样本空间,那么这两个集合的笛卡尔积将会组成一个新的样本空间,这个新的样本空间产生的随机变量以及随机变量的分布就是联合分布
离散联合分布 Discrete Joint Distribution
Definition Joint Distribution:Let X and Y be random variables,and consider the ordered pair(X,Y).If there are only finitely or at most countably many different possible values (x,y) for the pair (X,Y),then we say that x and Y have a discrete joint distribution
这里面又提到了可数的这个概念,可数无限的,和有限的样本空间通过笛卡尔积得到的新的有限的,或者可数的样本空间就是原始两个样本空间的联合分布。
举个🌰 :
扔一个均匀的骰子和一个均匀的硬币,将他们的结果组合起来会有下面这些结果组合:
硬币分为head 和tail,骰子是1~6点,其联合分布的结果如下表:
| Head | Tail | |
|---|---|---|
| 1 | $\frac{1}{12}$ | $\frac{1}{12}$ |
| 2 | $\frac{1}{12}$ | $\frac{1}{12}$ |
| 3 | $\frac{1}{12}$ | $\frac{1}{12}$ |
| 4 | $\frac{1}{12}$ | $\frac{1}{12}$ |
| 5 | $\frac{1}{12}$ | $\frac{1}{12}$ |
| 6 | $\frac{1}{12}$ | $\frac{1}{12}$ |
Theorem: Suppose that two random variable X and Y each have a discrete distribution.Then X and Y have a discrete joint distribution
证明主要分为两部分
- 如果两个样本空间有限,那么其笛卡尔积有限,这个是集合论中已经明确的结论了
- 如果两个样本空间可数无限,那么气笛卡尔积也是可数无限的,这个相关证明也在集合论中,这里不再证明
Definition Joint Probability Function,p.f. The joint probability function,or the joint p.f. of X and Y is defined as the function f such that for every point (x,y) in xy-plane:
$$
f(x,y)=Pr(X=x\text{ and } Y=y)
$$
这个定义是定义联合概率函数,对应一维随机变量里的概率函数,这个函数输入二维随机变量,产生一个实数概率值:$X\times Y\to \Re$
Theorem Let $X$ and $Y$ have a discrete joint distribution.If $(x,y)$ is not one of the possible values of the pair $(X,Y)$ the $f(x,y)=0$ .Also,
$$
\sum_{\text{All }(x,y)}f(x,y)
$$
Finally,for each set $C$ of ordered pairs
$$
Pr[(X,Y)\in C]=\sum_{(x,y)\in C}f(x,y)
$$
接着我们定义的是离散联合分布,以及通过新的规则 $(X,Y)\in C$ 产生一个新的分布。
还是上面第一个例子,如果我们把$C={c:x=\text{Head and } y\leq 3}$,那么这个新的联合事件的概率 :
$$
Pr[(X,Y)\in C]=\frac{1}{12}+\frac{1}{12}+\frac{1}{12}=\frac{1}{4}
$$
连续联合分布 Continuous Joint Distribution
进一步,我们就来到了两个连续随机变量的联合分布上了,相对于离散随机变量,连续随机变量在联合这个问题上难度将提升非常大。
先来个🌰 :
还是水费和电费的例子,我们之前解决是用几何的方法解决的,现在我们用分析的方式解决,回一下题干,“我们有一家工厂,每个月用水是在 $[10,110]$ 吨,用电在 $[100,1100]$ 千瓦时,并且是完全随机的均匀的,那么我们可以计算用水在 $[20,40]$ 吨,用电在 $[600,800]$ 千瓦时的概率是多少?”
用二重积分的方法,我们能求出联合分布面积,结合其概率密度分布$f(x,y)=\frac{1}{100000}$
$$
Pr[(X,Y)\in C]=\int_C\int \frac{1}{100000}dx dy
$$
这个只是算是微积分的一个简单应用,如果不知道为啥这么做,可以去看一下多重积分的基础知识就自然明白了,但是这个公式却可以延伸成为联合分布的定义。
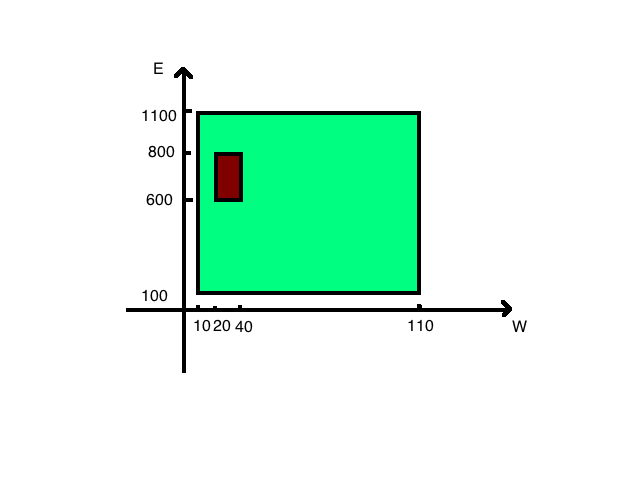
Definition Continuous Joint Distribution/Joint p.d.f./Support:Two random varibales X and Y have a continuous joint distribution if there exists a nonnegative function f defined over the entire xy-plane such that for every subset C of the plane,
$$
Pr[(X,Y)\in C]=\int_C\int f(x,y)dx dy
$$
if the integral exists.The function $f$ is called the joint probability density function(abbreviated joint p.d.f)of $X$ and $Y$.The closure of the set ${(x,y):f(x,y)>0}$ is called the support of (the distribution of) $(X,Y)$
关于连续随机变量联合分布的定义,和前面的连续随机变量第一非常像,这个定义只是告诉我们了外观,什么样的形式,但最核心的部分也就是那个函数$f$ 并没有告诉我们怎么得到的,是否能通过两个随机变量自有的分布计算得出,也就是我们假设连续随机变量X 有一个$g_1(x)$ 的连续分布函数,连续随机变量Y 有一个$g_2(y)$ 的连续分布函数,我们怎么从$g_1$和$g_2$ 得到$f$ ,他们之间具体有没有实质性的关系,我们留作一个思考。
其实单随机变量也没有给出其pdf的求法,而是直接制定了存在的某个连续函数,其要求满足一些性质,但是我们的联合pdf,应该在后续给出以下类似的性质。
A joint p.d.f. must satisfy the following two conditions:
$$
f(x,y)\geq 0 \text{ for } -\infty <x<\infty \text{ and } -\infty <y<\infty
$$
and
$$
\int^{\infty}_{-\infty}\int^{\infty}_{-\infty}f(x,y)dxdy=1
$$
所有满足上面这个性质的二元函数都能当联合pdf,其对应的某些 $X$ 和 $Y$ 概率分布。
由于 $X$ 和 $Y$ pdf不唯一,所以联合起来的pdf也不唯一。
联合连续分布的pdf的积分性质:
Theorem For every contimuous joint distribution on the xy-plane,the following two statements hold:
- Every individual point,and every infinite sequence of points,in the xy-plane has pribability 0.
- Let $f$ be a continuous function of one real variable defined on a(possibly unbounded) interval(a,b).The sets ${(x,y):y=f(x),a<x<b}$ and ${(x,y):x=f(y),a<y<b}$ have probability 0
直观的解释,就是继承自单连续随机变量的某个点的概率是0,延伸到二维空间,一个点的概率是0,每一个无限的点的序列概率也是0,二维空间上的一维函数对应的概率也是零,可以理解为二维分布上一条线(对应一维分布上的一个点)概率是0.
对于一条线,两个变量有一个被消去了,也就是从二重积分上来说微分部分是0,所以结果是0,从图形上来看,一个面的体积是0 。
混合二维分布 Mixed Bivariate Distribution
混合分布,一个连续的,一个离散的,结合了上述两种的全部特点,当然也有一些特例,我们先举个例子说明这种情况存在:比如我们选择特定的五个城市的气温情况,随机选择一个城市,是离散的,而城市温度可以看做一个连续的随机变量,那么这个试验就是一个混合的分布。
Definition Joint p.f/p.d.f: Let $X$ and $Y$ be random variables such that $X$ is discrete and $Y$ is continuous.Suppose that there is a function $f(x,y)$ define on the xy-plane such that,for every pair A and B of subsets of the real numbers
$$
Pr(X\in A \text{ and } Y \in B)=\int_B\sum_{x\in A}f(x,y)dy
$$
if the integral exists.Then the function $f$ is called the joint p.f./p.d.f of $X$ and $Y$
没错我们关注的焦点应该是那个联合分布函数(现在他既是连续又是离散的)只要积分存在,那么这个函数就是X 和Y的一个混合二维分布。
同样要满足下面这个雷打不动的性质,以满足柯氏公理:
$$
\int^{\infty}_{-\infty}\sum^{\infty}_{i=1}f(x_i,y)dy=1
$$
相对于离散的双重求和,连续分布的二重积分,混合分布的积分加求和应该是自然的。
当然我们可能想到可不可以交换求和和积分顺序,当然没什么问题(只是积分范围需要重新确定一下,这个问题属于微积分,计算的技巧比较强,但是还是要强调一下):
$$
(X,Y)\in C\\
\text{we set } C_x={y:(x,y)\in C}\\
\text{then } Pr((X,Y)\in C)=\sum_{\text{All } x}\int_{C_x}f(x,y)dy
$$
纯计算问题,在做二重积分的时候,比较麻烦的地方就是积分界的代换。
举个🌰 :
一个联合分布:
$$
f(x,p)=p^x(1-p)^{1-x}\text{ for } x=0,1 \text{ and } 0<p<1
$$
计算$Pr(X\leq 0 \text{ and } P\leq \frac{1}{2})$
解:
$$
Pr(X\leq 0 \text{ and } P\leq \frac{1}{2})=\int_0^{\frac{1}{2}}(1-p)dp\\
=-\frac{1}{2}[(1-\frac{1}{2})^2-(1-0)^2]=\frac{3}{8}
$$
二维累积分布函数 Bivariate Cumulative Distribution Functions
因为我们前面研究的离散分布,描述离散分布的工具就是一个概率函数,扩展到二维联合分布就是变成了一个二维的表,研究连续分布,工具是pdf,我们也研究过了,但是另一个能同时描述离散和连续分布的cdf还没研究其联合形式。
Definition: Joint(Cumulative) Distribution Function/c.d.f. The joint distribution function or joint cumulative distribution function (joint c.d.f) of two random variables X and Y is defined as the function F such that for all values of x and y( $-\infty<x<\infty$ and $-\infty<y<\infty$)
$$
F(x,y)=Pr(X\leq x \text{ and } Y\leq y )
$$
定义好像没什么稀奇的,就是一维的扩展版,但是有些性质变得复杂了,比如求一个区间的概率:
$$
Pr(a<x\leq b \text{ and } c<Y\leq d)\\
=Pr(a<X\leq b \text{ and } y\leq d) -Pr(a<x\leq b \text{ and } y\leq c)\\
=[Pr(X\leq b \text{ and } Y \leq d)-Pr(X\leq a \text{ and } Y \leq d)]-\\
[Pr(X\leq b \text{ and } Y \leq c)-Pr(X\leq a \text{ and } Y \leq c)]\\
=F(b,d)-F(a,d)-F(b,c)+F(a,c)
$$
这个过程可能画个平面图也能看的清楚些,用概率定义时候的定理也可以: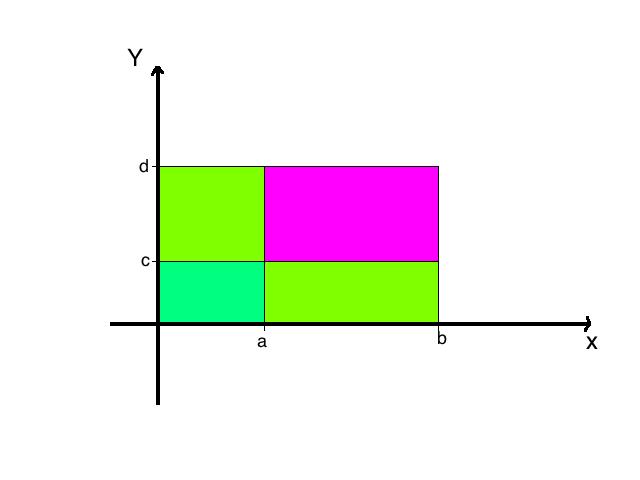
Theorem Let $X$ and $Y$ have a joint c.d.f. $F$.The c.d.f. $F_1$ of just the single random variable $X$ can be derived from the joint c.d.f. $F$ as $F_1(x)=lim_{y\to \infty}F(x,y)$.Similarly,the c.d.f. $F_2$ of $Y$ equals $F_2(y)=lim_{x\to \infty}F(x,y)$ ,for $0<y\leq \infty$
这个定理解决的问题是我们上面提到的关于如何把联合pdf拆分成单个变量的pdf,这个定理帮我们解决的是个相关的问题,就是把cdf拆成两个变量分别的cdf,具体做法就是对于二维联合cdf,对其中一个变量取极限得到的就是另一个变量的cdf。
证明如下,我们只证明其中一个,另一个将不证自明: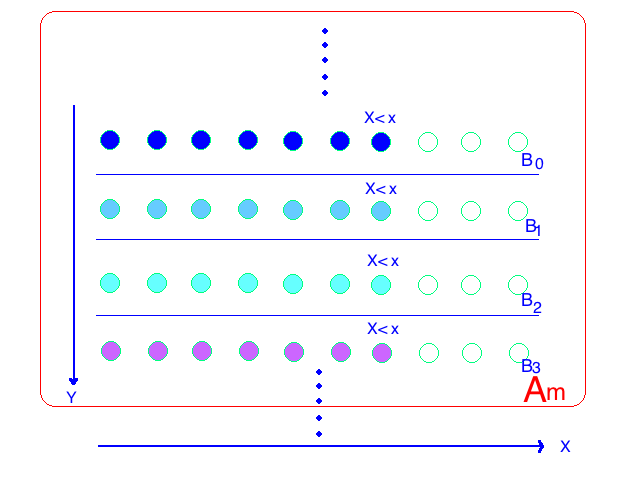
- 离散情况下:
$$
\text{Let }\\
B_0={X\leq x \text{ and } Y\leq 0} \\
B_1={X\leq x \text{ and }n-1<y\leq n}\text{ ,for } n=1,2\dots\\
A_m=\bigcup^{m}_{n=0}B_n\text{ ,for }m=1,2,\dots\\
$$
我们可以确定:${X\leq x}=\bigcup^{\infty}_{n=-0}B_n$ ,并且 $A_m={X\leq x \text{ and } Y\leq m} \text{ for } m=1,2,\dots$ 这样我们有 $Pr(A_m)=F(x,m) \text{ for each } m$
那么我们就有:
$$
F_1(x)=Pr(X\leq x)=Pr(\bigcup^{\infty}_{n=1}B_n)\\
=\sum^{\infty}_{n=0}Pr(B_n)=lim_{m\to \infty} Pr(A_m)\\
=lim_{m\to \infty}F(x,m)=lim_{y\to \infty}Pr(A_m)
$$
注意加法原理成立的必然条件B之间相互不想交,切所有B的集合是全集。
- 连续情况下:
这个证明就简单多了和上述证明基本一致,只要把求和编程就积分就可以证明连续情况下的结论
最后说一下joint cdf和joint pdf的关系,微积分关系😆
$$
F(x,y)=\int^y_{-\infty}\int^x_{-\infty}f(r,s)drds\\
f(x,y)=\frac{\partial^2F(x,y)}{\partial x\partial y}
$$
总结
我们从单变量逐步向更复杂更贴近现实应用的双变量联合分布靠近,得出了双变量联合分布的一些性质和工具,明天继续从联合分布进一步演化内容,待续。。
