Abstract: 矩阵对角化，以及对角化过程中引入的知识，以及对角化的应用
Keywords: Eigenvalues,Eigenvectors,Diagonalizing,Fibonacci Numbers, $A^k$ ,Nondiagonalizable Matrix

对角化

对角化一个矩阵，和之前个种各样的分解有一个同样的思路，当矩阵从原始形态通过各种计算性质变形成为各种有规则的，或者在数值上有特殊的性质，这些特殊的形状都可以用在不同问题上，比如LDR分解可以直接求出pivot值，求解方程，QR分解可以是通过变换向量空间的基来使向量某些方面的性质凸显出来。
今天说的对角化就是利用了特征值特征向量的计算性质，通过对 $Ax=\lambda x$ 进行变形引申得到的。而这个diagonalizing后的矩阵对于矩阵求幂有非常简单的计算。
假设 $n \times n$ 的矩阵 $A$ 有n个特征向量，那么我们把每个特征向量按照每列一个特征向量的组合方式形成一个矩阵，那么这个矩阵我们称之为 $S$

$$
AS=
A\begin{bmatrix}
\vdots &\dots &\vdots\\
x_1&\dots &x_n\\
\vdots &\dots &\vdots
\end{bmatrix}=
\begin{bmatrix}
\vdots &\dots &\vdots\\
Ax_1&\dots &Ax_n\\
\vdots &\dots &\vdots
\end{bmatrix}=
\begin{bmatrix}
\vdots &\dots &\vdots\\
\lambda_1 x_1&\dots &\lambda_n x_n\\
\vdots &\dots &\vdots
\end{bmatrix}\\
\begin{bmatrix}
\vdots &\dots &\vdots\\
\lambda_1 x_1&\dots &\lambda_n x_n\\
\vdots &\dots &\vdots
\end{bmatrix}=
\begin{bmatrix}
\vdots &\dots &\vdots\\
x_1&\dots &x_n\\
\vdots &\dots &\vdots
\end{bmatrix}\begin{bmatrix}
\lambda_1 & &\\
&\ddots &\\
&&\lambda_n
\end{bmatrix}=S\Lambda\\
so:
AS=S\Lambda\\
\Lambda=S^{-1}AS\\
A=S\Lambda S^{-1}
$$
$\Lambda$ 是 $\lambda$ 的大写，表示的是对角矩阵，每个元素都是eigenvalue。
如果矩阵A没有n个independence的eigenvector也是无法对角化的，上面的推到过程是属于两头堵的方式，先正向求出 $AS$ 的结果发现其结果和 $S\Lambda$ 结果一样，所以就得到了 $\Lambda$ 的表达式，下面我们我们就可以来计算 $A^k$ 了，利用上面推到过程中的最后一步，这个简直非常完美了
$$
A^k=A\cdot A\dots A=S \Lambda S^{-1} S \Lambda S^{-1} \cdots S \Lambda S^{-1}=S \Lambda \Lambda \cdots \Lambda S^{-1}=S \Lambda^k S^{-1}
$$
一个矩阵的k次幂等于其对角矩阵的k次幂– $S \Lambda^k S^{-1}$
我们可以回忆下上一篇，我们求过一个矩阵的k次方乘以一个向量 $A^ky$ ,用特征向量来作为 $y$ 的基，然后写成
$$
A^k:\\
suppose: \;C=\begin{bmatrix}c_1 &\dots & c_n\end{bmatrix}\\
y=c_1 x_1+c_2 x_2+\dots +c_n x_n=SC \\
A^k y=A^k(c_1 x_1+c_2 x_2+\dots +c_n x_n)\\
=c_1A^kx_1+c_2A^kx_2+\dots +c_nA^kx_n\\
=c_1\lambda_1^k x_1+c_2\lambda_2^k x_2+\dots + c_n\lambda_n^k x_n\\
=S\Lambda^k C
$$

上面这个是回忆上一篇的内容同时通过这篇的内容加以结合，也是 $A^k$ 小节的主要过程，就得到了对角矩阵的一个应用，原理一致，方法不同而已，最终的理论根基都是 $Ax=\lambda x$这个是本章最核心的方程，没有之一，就是最核心的，而且本章作为线性代数的高潮部分，这个方程也可以称之为线性代数中最重要的方程之一。

在使用 $\Lambda$ 之前，我们有几个remark需要强调一下：

没有重复特征值的矩阵可以被对角化
特征向量可以任意乘以一个非零常数（长度可以缩放）
对角矩阵中特征值的顺序与S中特征向量的排列顺序对应
有些矩阵没有足够的eigenvalue，所以也没有足够的eigenvector来组成S，这类矩阵不能被对角化。

注意矩阵对角化和是否可逆没有直接关系

可逆表示需要行列式非零，行列式非零对特征值是有影响的，表明特征值不能为0
可对角化是说特征向量必须足够，也就是不能有特征向量缺失，$n \times n$ 就应该有n个特征向量

一个重要的结论：如果有n个不同的eigenvalues，那么就会对应有n个independence 的eigenvectors，那么这个矩阵可以被对角化;也就是说，如果矩阵有n个不同的eigenvalue，那么矩阵可以被对角化
证明 $2\times 2$ 矩阵的情况 :
$$
Suppose :\\
c_1x_1+c_2x_2=0\\
A(c_1x_1+c_2x_2)=0\\
c_1Ax_1+c_2Ax_2=0\\
\lambda_1 c_1x_1+\lambda_2 c_2x_2=0\\
\lambda_1(c_1x_1+c_2x_2)=0\\
so:\\
\lambda_1 c_1x_1+\lambda_2 c_2x_2 - \lambda_1(c_1x_1+c_2x_2)=0\\
(\lambda_2 - \lambda_1 )c_2x_2=0\\
for:\\
\lambda_2 \neq \lambda_1 \\
so:\\
c_2=0\\
similarly:\\
c_1=0
$$
那么一开始的假设中只有 $c_1=0$ 和 $c_2=0$ 满足 $c_1x_1+c_2x_2=0$ 也就是说 $x_1,x_2$ 线性无关
证明可以直接被推广到多维。
这个证明很是巧妙，以至于我也看了半天才明白套路，通过利用特征向量和矩阵相乘得到特征值的性质，以及nullspace的性质来证明，不同的特征值对应的特征向量彼此之间独立。
通过对角化的方法可以轻松得出markov矩阵的性质，一个特征值为1，那么它对应的特征向量在k次幂后是稳定的，另一个小于1的将会被消灭。
那么什么时候$A^k$会自我毁灭，没错，如果矩阵的所有特征值都小于1，那么就毁灭了 $|\lambda|<1$

斐波那契数列(Fibonacci Numbers)

斐波那契数列，高中的时候学的生兔子什么的，之前新闻上还说有个女博士用这玩意炒股，赚到翻，然后，C语言刚学了一个月的时候，老师说能把这个做出来说明学的不错了，不过好像确实不太好写，我们来段代码，我们用python来写一下试试：

N=10
a=1
b=1
print a
print b
for i in range(N-2):
    c=a+b
    a=b
    b=c
    print c

输出：

通过计算机程序可以很快的得到任意项的结果，但是从数学的角度，我们也很关心他的增长率，也就是他是怎么增长的？线性？二次？还是指数增长？
Fibonacci Numbers用递归公式来表示：
$$
a_n=a_{n-1}+a_{n-2} \,\, where\,\,n>2
$$
如果我们把这个递归关系写成矩阵形式，首先，我们需要弄个方阵出来，搞两个向量不太靠谱，没办法对角化，所以我们加一个
$$
\begin{bmatrix}a_n\\a_{n-1}\end{bmatrix}=
\begin{bmatrix}1&1\\1&0\end{bmatrix}\begin{bmatrix}a_{n-1}\\a_{n-2}\end{bmatrix}
$$
这个可以叫做矩阵形式的递归，通过 $\begin{bmatrix}a_{n-1}\\a_{n-2}\end{bmatrix}$ 来推导出 $\begin{bmatrix}a_n\\a_{n-1}\end{bmatrix}$ 递归得出，而中间的系数就比较有趣了，因为我们可以得出
$$
\begin{bmatrix}a_n\\a_{n-1}\end{bmatrix}=
\begin{bmatrix}1&1\\1&0\end{bmatrix}^{n-1}\begin{bmatrix}a_2\\a_1\end{bmatrix} \, where \, n>2
$$
这样问题就转换到 $A^k$ 的问题上了
$$
A=\begin{bmatrix}1&1\\1&0\end{bmatrix}\\
$$
求A的特征值，特征向量
$$
Ax=\lambda x\\
det(\begin{bmatrix}1-\lambda &1\\1&0-\lambda\end{bmatrix})=0\\
\lambda^2-\lambda-1=0\\
\lambda_1=\frac{1+\sqrt{5}}{2} \approx 1.618 \\
\lambda_2=\frac{1-\sqrt{5}}{2} \approx -.618 \\
x_1=\begin{bmatrix}\frac{1+\sqrt{5}}{2}\\1\end{bmatrix}\\
x_2=\begin{bmatrix}\frac{1-\sqrt{5}}{2}\\1\end{bmatrix}
$$
Fibonnaci 数列的递归系数矩阵的特征值是黄金分割比！是不是很神奇！也就是说矩阵在k次后 $\lambda_1$ 将会成为主要的增长系数 $\lambda_2$ 由于小于1 将会被消灭。
比如100次方后将约等于
$$
\begin{bmatrix}1\\0\end{bmatrix}=c_1x_1+c_2x_2=
c_1\begin{bmatrix}\frac{1+\sqrt{5}}{2}\\1\end{bmatrix}+
c_2\begin{bmatrix}\frac{1-\sqrt{5}}{2}\\1\end{bmatrix}\\
c_1=\frac{1}{\sqrt{5}}\\
c_2=-\frac{1}{\sqrt{5}}\\
\begin{bmatrix}a_{100}\\a_{99}\end{bmatrix}=\frac{1}{\sqrt{5}} \lambda_1^{99}x_1-\frac{1}{\sqrt{5}} \lambda_2^{99}x_2=\frac{1}{\sqrt{5}} \lambda_1^{99}\begin{bmatrix}\frac{1+\sqrt{5}}{2}\\1\end{bmatrix}\\
a_{100}=\frac{1}{\sqrt{5}}(\frac{1+\sqrt{5}}{2})^{99}\frac{1+\sqrt{5}}{2}=3.534\times 10^{20}
$$
检验一下：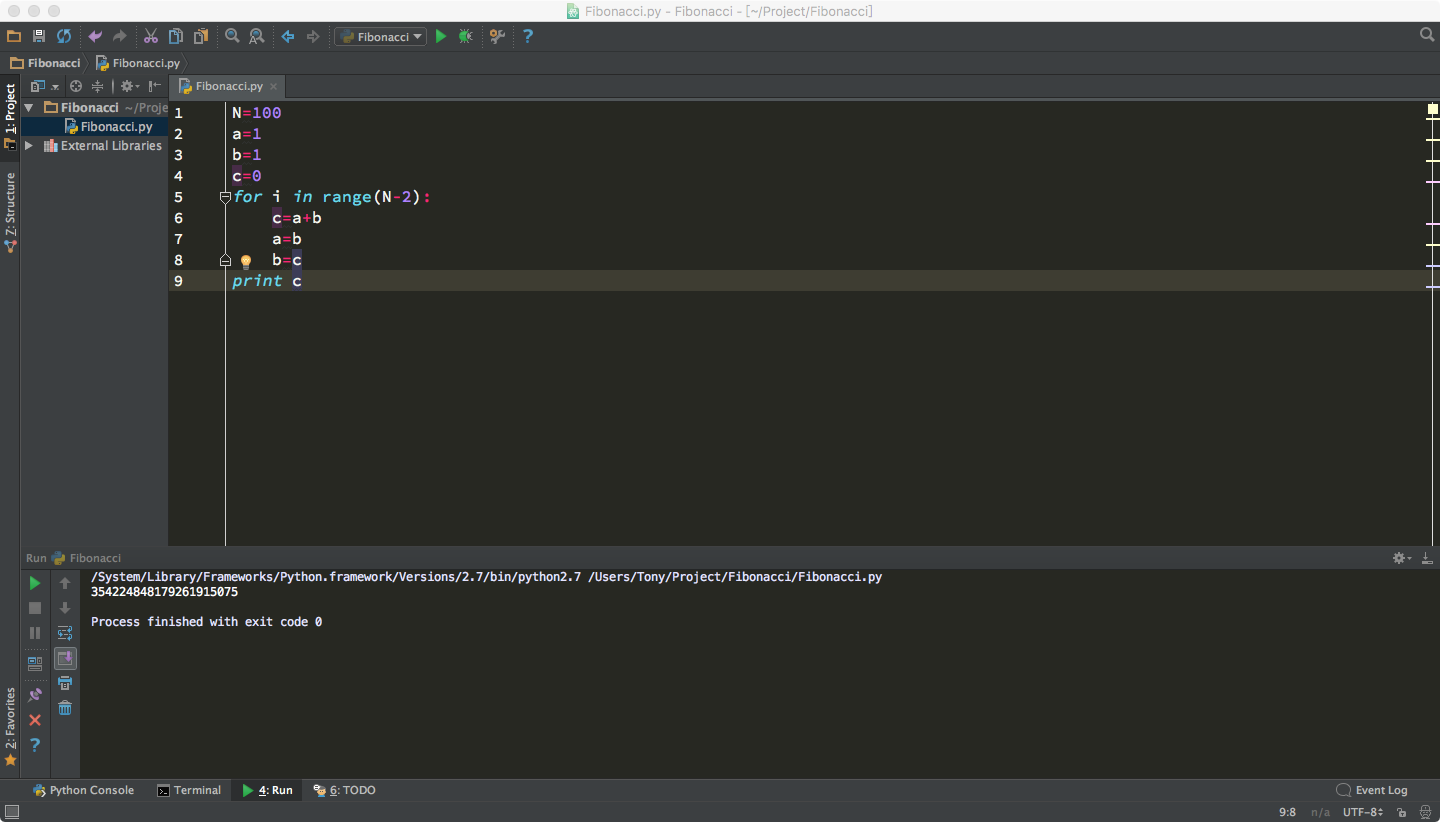

基本一致

矩阵求幂 $A^k$

Fibonnaci Numbers是一个典型的差分方程 $u_{k+1}=Au_k$ Solution is $u_k=A^ku_0$ 这就是一个典型的解过程，关键环节就是 $A^k$ ,过程和上面解决问题的关键步骤一般分为三步：

分解成以特征向量为基的线性组合 $u_0=Sc$
Multiplies $\Lambda^k$
$u_k=\sum c_i(\lambda_i)^kx_i$ 求解S和 $\Lambda^k$ 和 $S^{-1}u_0$ 的积

所以:
$$
A^ku_0=S\Lambda^kS^{-1}u_0=S\Lambda^kc\\
u_k=c_1(\lambda_1)^kx_1+\dots + c_n(\lambda_n)^kx_n
$$
这个就是 $u_k=Au_{k-1}$的解

所以我们的对于这种迭代关系是线性的差分方程，解法就是通过将初始条件分解成特征向量的线性组成，然后通过特征值的幂和特征向量矩阵的组合，得到解。
transforming to an eigenvector basis 是一种非常经典的做法，比如傅里叶级数都是典型应用。

非对角化矩阵

并不是所有的矩阵都能对角化的，前面也说了，有些特征值重复或者有些解不存在的时候，那么如何判断是否可以对角化呢？（就像判断是否可逆的那种方法）
我们可以考察两种指标来确定是否能对角化

Geometric Multiplicity=GM ,计算线性独立的eigenvector 的数量，也就是$A-\lambda I$ 的nullspace 的维度
Algebra Multiplicity=AM ,计算重复的 $\lambda$ 主要考察 $det(A-\lambda I)=0$ 的解

GM和AM保持关系 $GM \leq AM$
当$GM < AM$ 时矩阵不可对角化

$AB$ 和 $A+B$ 的特征值

特征值是否满足线性呢？不满足，笨方法也能看出来这根本不是一路的：
$$
ABx=A\beta x=\beta Ax=\beta \lambda x\\
$$
上面明显有问题，看出来问题在哪了么？
式子$Ax=\lambda x$当且仅当 x是A的特征向量的时候
所以 $A\beta x=\beta Ax=\beta \lambda x$ 这一步并不是对于所有矩阵都满足，只有A，B矩阵的特征向量相同的时候才能相等

Commuting Matrix share eigenvectors ,假设，如果A和B能够被对角化，他们拥有完全相同的特征向量，当且仅当 $AB=BA$

证明方法：
$$
ABx=A\beta x=\beta Ax=\beta \lambda x \\
\beta \lambda x=\lambda\beta x=\lambda Bx=B\lambda x=BAx\\
ABx=BAx\\
AB=BA
$$

对于A+B同理，只有当A和B的特征向量一致的时候，才能完成加法。
另外一个重要应用可以参考量子力学，Heisenberg’s uncertainty principle

Conclusion

本文主要讲解矩阵对角化，对角化的应用，对角化应该是在应用中最长用到的矩阵处理方法，所以用了一天的时间写了这一篇文章，希望能帮助理解。

人工智能基础

【线性代数】6-2:对角化(Diagonalizing a Matrix)

对角化

对角化

斐波那契数列(Fibonacci Numbers)

矩阵求幂 $A^k$

非对角化矩阵

$AB$ 和 $A+B$ 的特征值

Conclusion